Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(A=lim\frac{\sqrt{n+2}+\sqrt{n+1}}{1}=lim\left[n\left(\sqrt{1+\frac{2}{n}}+\sqrt{1+\frac{1}{n}}\right)\right]=+\infty.2=+\infty\)
\(B=lim\frac{8^3.64^n-9.27^n}{4^4.64^n+5^3.25^n}=\frac{8^3-9.\left(\frac{27}{64}\right)^n}{4^4+5^3\left(\frac{25}{64}\right)^n}=\frac{8^3}{4^4}=2\)
\(1;-\frac{1}{2};\frac{1}{4}...\) là dãy cấp số nhân lùi vô hạn có \(u_1=1\) và \(q=-\frac{1}{2}\)
Do \(\left|q\right|< 1\) nên theo công thức tổng cấp số nhân:
\(S_n=\frac{u_1}{1-q}=\frac{1}{1+\frac{1}{2}}=\frac{2}{3}\)
a) Với n = 1, vế trái chỉ có một số hạng là 2, vế phải bằng = 2
Vậy hệ thức đúng với n = 1.
Đặt vế trái bằng Sn.
Giả sử đẳng thức a) đúng với n = k ≥ 1, tức là
Sk= 2 + 5 + 8 + …+ 3k – 1 =
Ta phải chứng minh rằng cũng đúng với n = k + 1, nghĩa là phải chứng minh
Sk+1 = 2 + 5 + 8 + ….+ 3k -1 + (3(k + 1) – 1) =
Thật vậy, từ giả thiết quy nạp, ta có: Sk+1 = Sk + 3k + 2 = + 3k + 2
=
(điều phải chứng minh)
Vậy theo nguyên lí quy nạp toán học, hệ thức đúng với mọi n ε N*
b) Với n = 1, vế trái bằng , vế phải bằng
, do đó hệ thức đúng.
Đặt vế trái bằng Sn.
Giả sử hệ thức đúng với n = k ≥ 1, tức là
Ta phải chứng minh .
Thật vậy, từ giả thiết quy nạp, ta có:
= (điều phải chứng minh)
Vậy theo nguyên lí quy nạp toán học, hệ thức b) đúng với mọi n ε N*
c) Với n = 1, vế trái bằng 1, vế phải bằng = 1 nên hệ thức đúng với n = 1.
Đặt vế trái bằng Sn.
Giả sử hệ thức c) đúng với n = k ≥ 1, tức là
Sk = 12 + 22 + 32 + …+ k2 =
Ta phải chứng minh
Thật vậy, từ giả thiết quy nạp ta có:
Sk+1 = Sk + (k + 1)2 = = (k + 1).
= (k + 1)
(đpcm)
Vậy theo nguyên lí quy nạp toán học, hệ thức đúng với mọi n ε N*
a/ \(=lim\frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{1}{\infty}=0\)
b/ \(=lim\frac{6n+1}{\sqrt{n^2+5n+1}+\sqrt{n^2-n}}=\frac{6+\frac{1}{n}}{\sqrt{1+\frac{5}{n}+\frac{1}{n^2}}+\sqrt{1-\frac{1}{n}}}=\frac{6}{1+1}=3\)
c/ \(=lim\frac{6n-9}{\sqrt{3n^2+2n-1}+\sqrt{3n^2-4n+8}}=lim\frac{6-\frac{9}{n}}{\sqrt{3+\frac{2}{n}-\frac{1}{n^2}}+\sqrt{3-\frac{4}{n}+\frac{8}{n^2}}}=\frac{6}{\sqrt{3}+\sqrt{3}}=\sqrt{3}\)
d/ \(=lim\frac{\left(\frac{2}{6}\right)^n+1-4\left(\frac{4}{6}\right)^n}{\left(\frac{3}{6}\right)^n+6}=\frac{1}{6}\)
e/ \(=lim\frac{\left(\frac{3}{5}\right)^n-\left(\frac{4}{5}\right)^n+1}{\left(\frac{3}{5}\right)^n+\left(\frac{4}{5}\right)^n-1}=\frac{1}{-1}=-1\)
f/ Ta có công thức:
\(1+3+...+\left(2n+1\right)^2=\left(n+1\right)^2\)
\(\Rightarrow lim\frac{1+3+...+2n+1}{3n^2+4}=lim\frac{\left(n+1\right)^2}{3n^2+4}=lim\frac{\left(1+\frac{1}{n}\right)^2}{3+\frac{4}{n^2}}=\frac{1}{3}\)
g/ \(=lim\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n}-\frac{1}{n+1}\right)=lim\left(1-\frac{1}{n+1}\right)=1-0=1\)
h/ Ta có: \(1^2+2^2+...+n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}\)
\(\Rightarrow lim\frac{n\left(n+1\right)\left(2n+1\right)}{6n\left(n+1\right)\left(n+2\right)}=lim\frac{2n+1}{6n+12}=lim\frac{2+\frac{1}{n}}{6+\frac{12}{n}}=\frac{2}{6}=\frac{1}{3}\)
Nhanh nhất là sử dụng công thức tổng cấp số nhân với \(u_1=\frac{1}{2}\) và công bội \(q=\frac{1}{2}\) , khỏi cần quy nạp mất thời gian:
\(S_n=\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2^n}=u_1.\frac{1-q^n}{1-q}=\frac{1}{2}\left(\frac{1-\frac{1}{2^n}}{1-\frac{1}{2}}\right)=1-\frac{1}{2^n}=\frac{2^n-1}{2^n}\)
Ta có : \(S=\left(4+2+\frac{1}{4}\right)+\left(16+2+\frac{1}{16}\right)+..+\left(2^{2n}+2+\frac{1}{2^{2n}}\right)\)
\(=\left(4+16+...+2^{2n}\right)+2n+\left(\frac{1}{4}+\frac{1}{16}+.....+\frac{1}{2^{2n}}\right)\)
Áp dụng công thức tính tổng của n số hạng đầu của một cấp số nhân \(S_n=u_1\frac{q^n-1}{q-1}\)
\(S=4.\frac{4^{n-1}}{3}+2n+\frac{1}{4}.\frac{2^{\frac{1}{2n}}-1}{\frac{1}{4}-1}=4.\frac{4^n-1}{3}+2n+\frac{1}{3}.\frac{2^{2n}-1}{2^{2n}}\)
\(=2n+\frac{4^n-1}{3}.\frac{4.4^n+1}{4^n}=2n+\frac{\left(4^n-1\right)\left(4^{n+1}+1\right)}{3.4^n}\)
a) \(\lim \frac{{2{n^2} + 6n + 1}}{{8{n^2} + 5}} = \lim \frac{{{n^2}\left( {2 + \frac{6}{n} + \frac{1}{{{n^2}}}} \right)}}{{{n^2}\left( {8 + \frac{5}{{{n^2}}}} \right)}} = \lim \frac{{2 + \frac{6}{n} + \frac{1}{n}}}{{8 + \frac{5}{n}}} = \frac{2}{8} = \frac{1}{4}\)
b) \(\lim \frac{{4{n^2} - 3n + 1}}{{ - 3{n^3} + 6{n^2} - 2}} = \lim \frac{{{n^3}\left( {\frac{4}{n} - \frac{3}{{{n^2}}} + \frac{1}{{{n^3}}}} \right)}}{{{n^3}\left( { - 3 + \frac{6}{n} - \frac{2}{{{n^3}}}} \right)}} = \lim \frac{{\frac{4}{n} - \frac{3}{{{n^2}}} + \frac{1}{{{n^3}}}}}{{ - 3 + \frac{6}{n} - \frac{2}{{{n^3}}}}} = \frac{{0 - 0 + 0}}{{ - 3 + 0 - 0}} = 0\).
c) \(\lim \frac{{\sqrt {4{n^2} - n + 3} }}{{8n - 5}} = \lim \frac{{n\sqrt {4 - \frac{1}{n} + \frac{3}{{{n^2}}}} }}{{n\left( {8 - \frac{5}{n}} \right)}} = \frac{{\sqrt {4 - 0 + 0} }}{{8 - 0}} = \frac{2}{8} = \frac{1}{4}\).
d) \(\lim \left( {4 - \frac{{{2^{{\rm{n}} + 1}}}}{{{3^{\rm{n}}}}}} \right) = \lim \left( {4 - 2 \cdot {{\left( {\frac{2}{3}} \right)}^{\rm{n}}}} \right) = 4 - 2.0 = 4\).
e) \(\lim \frac{{{{4.5}^{\rm{n}}} + {2^{{\rm{n}} + 2}}}}{{{{6.5}^{\rm{n}}}}} = \lim \frac{{{{4.5}^{\rm{n}}} + {2^2}{{.2}^{\rm{n}}}}}{{{{6.5}^{\rm{n}}}}} = \lim \frac{{{5^n}.\left[ {4 + 4.{{\left( {\frac{2}{5}} \right)}^{\rm{n}}}} \right]}}{{{{6.5}^n}}} = \lim \frac{{4 + 4.{{\left( {\frac{2}{5}} \right)}^{\rm{n}}}}}{6} = \frac{{4 + 4.0}}{6} = \frac{2}{3}\).
g) \(\lim \frac{{2 + \frac{4}{{{n^3}}}}}{{{6^{\rm{n}}}}} = \lim \left( {2 + \frac{4}{{{{\rm{n}}^3}}}} \right).\lim {\left( {\frac{1}{6}} \right)^{\rm{n}}} = \left( {2 + 0} \right).0 = 0\).
\(\lim\dfrac{2^{n}(4^{n+1}-3^{n+2}-1)}{5^{n}+8^{n}} =\lim\dfrac{4.8^{n}-9.6^{n}-2^{n}}{5^{n}+8^{n}} =\lim\dfrac{4-9.(\dfrac{6}{8})^{n}-(\dfrac{2}{8})^{n}}{(\dfrac{5}{8})^{n}+1} =\lim\dfrac{4-9.0-0}{0+1} =4\)
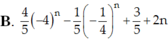
Chọn D.
Ta có:
- Có dãy số -22, 24, …, (-1)n.22n là cấp số nhân với n số hạng, có số hạng đầu u1 = -4 và công bội q = -4.
Do đó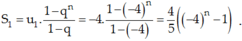
- Có dãy số
là cấp số nhân với n số hạng, có số hạng đầu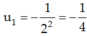 
và công bội q = -1/4.
Do đó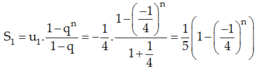
Vậy
