Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Gọi S là diện tích hình phẳng cần tìm. Đó f x > 0 , ∀ x ∈ 1 ; e 2 nên
S = ∫ 1 e 2 f x d x = ∫ 1 e 2 x + 1 ln x d x
Đặt
u = ln x d v = x + 1 d x ⇒ d u = 1 x d x v = 2 3 x x + x
Khi đó
S = 2 x 3 + 1 x ln x 1 e 2 - ∫ 1 e 2 2 x 3 + 1 d x = 8 e 3 + 8 e 2 + 13 9
Đáp án D

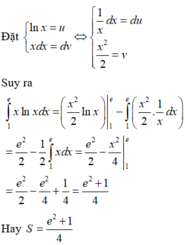

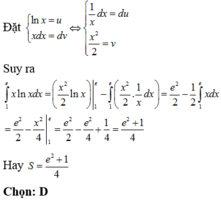
Gọi S là diện tích hình phẳng cần tìm. Do f(x) > 0 ∀ x ∈ 1 ; e 2
nên S = ∫ 1 e 2 f x d x = ∫ 1 e 2 x + 1 x d x
Đặt u = ln x d v = x + 1 d x ⇒ d u = 1 x d x v = 2 3 x x + x
Khi đó
S = 2 x 3 + 1 x ln x 1 e 2 - ∫ 1 e 2 2 x 3 + 1 d x
= 8 e 3 + 9 e 2 + 13 9
Đáp án D