K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MA
1
LH
4
5 tháng 12 2016
Ta có vì x, y là các số tự nhiên nên
\(\hept{\begin{cases}3xy\ge0\left(1\right)\\2x\ge0\left(2\right)\\2y\ge0\left(3\right)\end{cases}}\)
Từ đó ta có
\(3xy+2x+2y\ge0\)
Dấu = xảy ra khi \(x=y=0\)
TQ
6
TQ
0
TQ
2
28 tháng 10 2016
3xy + 2x + 2y = 0
=> x.(3y + 2) = -2y
=> \(x=\frac{-2y}{3y+2}\)
Do \(x\in N\Rightarrow3y+2\inƯ\left(-2y\right)\)
Mà 3y + 2 > -2y do y ϵ N => -2y = 0
=> y = 0; x = 0
Vậy x = y = 0
TN
0
10 tháng 10 2018
Bài này thêm điều kiện là: x,y thuộc Z nha ko là ko lm đc đâu
a, (x+5)(y-3)=15
| x+5 | -15 | -5 | -3 | -1 | 1 | 3 | 5 | 15 |
| y-3 | -1 | -3 | -5 | -15 | 15 | 5 | 3 | 1 |
| x | -20 | -10 | -8 | -6 | -4 | -2 | 0 | 10 |
| y | 2 | 0 | -2 | -12 | 18 | 8 | 6 | 4 |
Vậy có 8 cặp(x;y):...
các ý còn lại tương tự
F
16 tháng 10 2019
Bài giải
Mình làm câu a các câu b , d bạn làm tương tự nha !
a, \(\left(x+5\right)\left(y-3\right)=15\)
\(\Rightarrow\text{ }x+5\text{ , }y-3\inƯ\left(15\right)\)
| x + 5 | - 1 | 1 | - 3 | 3 | - 5 | 5 | - 15 | 15 |
| y - 3 | - 15 | 15 | - 5 | 5 | - 3 | 3 | - 1 | 1 |
| x | - 6 | - 4 | - 8 | - 2 | - 10 | 0 | - 20 | 10 |
| y | - 12 | 18 | - 2 | 8 | 0 | 6 | - 2 | 4 |
Vậy các cặp \(\left(x,y\right)=\text{ }...\)
c, \(xy+y+x=30\)
\(y\left(x+1\right)+x=30\)
\(y\left(x+1\right)+\left(x+1\right)=31\)
\(\left(y+1\right)\left(x+1\right)=31\)
Đến đây làm tương tự câu a nha !
Câu e để mình nghĩ tí đã nha !
TC
1
AH
Akai Haruma
Giáo viên
24 tháng 9 2023
Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau: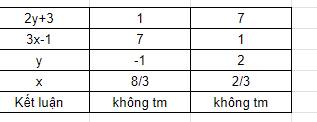
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.
x^3+y^3=3xy-1
x^3+y^3-3xy+1=0
(x+y)^3-3xy(x+y)-3xy+1=0
(x+y+1)(x^2+2xy+y^2-x-y+1)-3xy(x+y+1)=0
(x+y+1)(x^2+2xy+y^2-x-y+1-3xy)=0
suy ra +)x+y+1=0.VÌ x,y thuộc N* nên x+y+1 khác 0
+)x^2-xy+y^2+1-x-y=0
2(x^2-xy+y^2+1-x-y)=0
2x^2-2xy+2y^2+2-2x-2y=0
(x^2-2xy+y^2)+(x^2-2x+1)+(y^2-2y+1)=0
(x-y)^2+(x-1)^2+(y-1)^2=0
suy ra +)x-y=0
+)x-1=0
+)y-1=0
Vậy x=y=1