Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 :
a, ĐKXĐ : \(\dfrac{2x+1}{x^2+1}\ge0\)
Mà \(x^2+1\ge1>0\)
\(\Rightarrow2x+1\ge0\)
\(\Rightarrow x\ge-\dfrac{1}{2}\)
Vậy ...
b, Ta có : \(\sqrt[3]{-27}+\sqrt[3]{64}-\sqrt[3]{-\dfrac{128}{2}}\)
\(=-3+4-\left(-4\right)=-3+4+4=5\)
Bài 2 :
\(a,=2\sqrt{5}+6\sqrt{5}+5\sqrt{5}-12\sqrt{5}\)
\(=\sqrt{5}\left(2+6+5-12\right)=\sqrt{2}\)
\(b,=\sqrt{5}+\sqrt{5}+\left|\sqrt{5}-2\right|\)
\(=2\sqrt{5}+\sqrt{5}-2=3\sqrt{5}-2\)
\(c,=\dfrac{\left(5+\sqrt{5}\right)^2+\left(5-\sqrt{5}\right)^2}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}\)
\(=\dfrac{25+10\sqrt{5}+5+25-10\sqrt{5}+5}{25-5}\)
\(=3\)

- \(\sqrt{\frac{2x^2+1}{7x}}\)ĐK \(\hept{\begin{cases}\frac{2x^2+1}{7x}\ge0\\x\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}x>0\\x\ne0\end{cases}\Leftrightarrow}x>0}\)
- \(\frac{\sqrt{2x-1}}{x^2-9}=\frac{\sqrt{2x-1}}{\left(x-3\right)\left(x+3\right)}\)ĐK \(\hept{\begin{cases}2x-1\ge0\\\left(x-3\right)\left(x+3\right)\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge\frac{1}{2}\\x\ne3\\x\ne-3\end{cases}\Leftrightarrow}\hept{\begin{cases}x\ge\frac{1}{2}\\x\ne3\end{cases}}}\)
- \(\sqrt{\frac{x+2}{5-x}}\)ĐK \(\hept{\begin{cases}\frac{x+2}{5-x}\ge0\\5-x\ne0\end{cases}}\)
- \(TH1:\hept{\begin{cases}x+2\ge0\\5-x>0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge-2\\x< 5\end{cases}\Leftrightarrow}-2\le x< 5}\)
- \(TH2:\hept{\begin{cases}x+2\le0\\5-x< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\le-2\\x>5\end{cases}VN}\)
Vậy đk là : \(-2\le x< 5\)

Bài 1 : Để biểu thức có nghĩa -2x >= 0 <=> x =< 0
Bài 2 : Để biểu thức có nghĩa 2x - 6 >= 0 <=> x >= 3

a: ĐKXĐ: x>=0
b: ĐKXĐ: x-1>0 và -(x2-x-6)>=0
=>x>1 và (x-3)(x+2)<=0
=>x>1 và -2<=x<=3
=>1<x<=3

1) \(\frac{1}{\sqrt{2x-1}}\)có nghĩa khi \(\hept{\begin{cases}2x-1\ge0\\\sqrt{2x-1}\ne0\end{cases}}\)
\(\Leftrightarrow2x-1>0\)
\(\Leftrightarrow x>\frac{1}{2}\)
\(\sqrt{5-x}\)có nghĩa khi \(5-x\ge0\Leftrightarrow x\ge5\)
Vậy \(ĐKXĐ:\frac{1}{2}>x\ge5\)
2) \(\sqrt{x-\frac{1}{x}}\)có nghĩa khi \(\hept{\begin{cases}x-\frac{1}{x}\ge0\\x>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{x^2}{x}-\frac{1}{x}\ge0\\x>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{x^2-1}{x}\ge0\\x>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2-1\ge0\\x>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2\ge1\\x>0\end{cases}}\)
Vậy \(ĐKXĐ:x\ge1\)
3) \(\sqrt{2x-1}\)có nghĩa khi \(2x-1\ge0\) \(\Leftrightarrow x\ge\frac{1}{2}\)
\(\sqrt{4-x^2}\)có nghĩa khi \(4-x^2\ge0\Leftrightarrow x^2\le4\Leftrightarrow x\le2\)
Vậy \(ĐKXĐ:\frac{1}{2}\le x\le2\)
4) \(\sqrt{x^2-1}\)có nghĩa khi \(x^2-1\ge0\Leftrightarrow x^2\ge1\Leftrightarrow x\ge1\)
\(\sqrt{9-x^2}\)có nghĩa khi \(9-x^2\ge0\Leftrightarrow x^2\le9\Leftrightarrow x\le3\)
Vậy \(ĐKXĐ:1\le x\le3\)
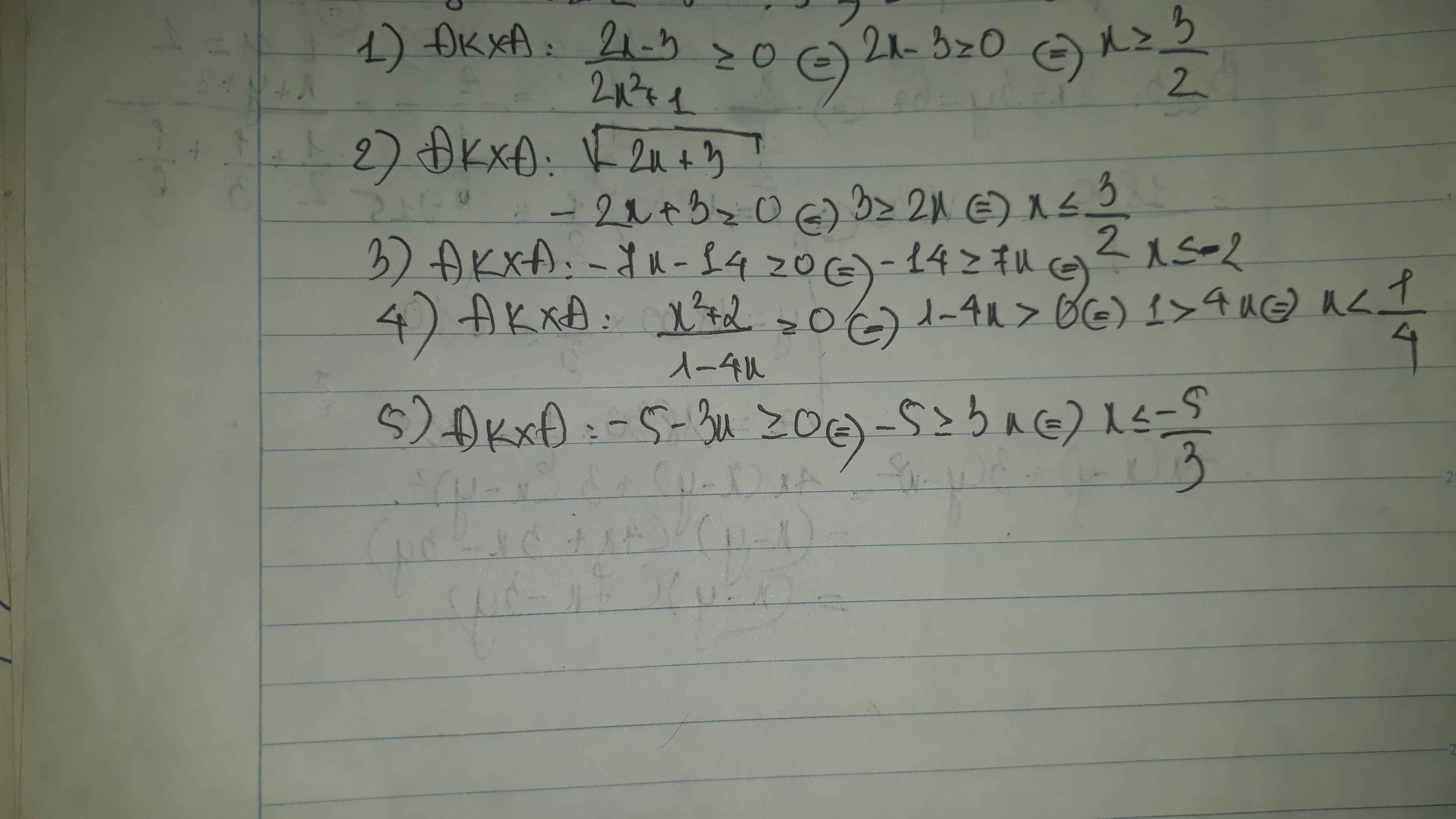
ĐKXĐ: \(\left\{{}\begin{matrix}2x-3>0\\5-2x>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{3}{2}\\x< \dfrac{5}{2}\end{matrix}\right.\)