CD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
18 tháng 4 2017
Vì khối lượng dâu y(kg) tỉ lệ thuận với khối lwọng đwòng x(kg) nên ta có \(y=kx\)
Theo điều kiện đề bài y = 2 thì x = 3, thay vào công thức ta đwọc 2 = k.3 nên k = \(\dfrac{2}{3}\)
Công thức trở thành y = \(\dfrac{2}{3}x\)
Khi y = 2,5 thì x = \(\dfrac{3}{2}y=\dfrac{3}{2}.2,5=3,75\)
Vậy hạnh nói đúng.
DD
18 tháng 4 2017
Vì khối lượng dâu y(kg) tỉ lệ thuận với khối lượng đường x(kg) nên ta có y = kx.
Theo đề ta có: y = 2 và x = 3
Thay vào công thức ta được 2 = k.3
=> k = \(\dfrac{2}{3}\)
Công thức trở thành y = \(\dfrac{2}{3}\)x
Thay y = 2,5 vào y = \(\dfrac{2}{3}\)x
=> 2,5 = \(\dfrac{2}{3}\)x
=>x = 2,5 . \(\dfrac{3}{2}\)
=>x = 3.75
Vậy Hạnh nói đúng
Thông cảm mk bị cận!
20 tháng 10 2017
BT1.
Ta có: \(2009^{20}=2009^{10}\times2009^2\)và \(20092009^{10}=2009^{10}\times10001^{10}\)
Rõ ràng \(2009^2< 10001^{10}\\ \Rightarrow2009^{10}\times2009^2< 2009^{10}\times10001^{10}\\ \Rightarrow2009^{20}< 20092009^{10}\left(đpcm\right)\)
BT9. Bn xem lại đề bài đi. \(x^2+x+1\) luôn lớn hơn 0 mà bn.
BT3.
Giả sử \(M\in N\)
Nên:
\(\left\{{}\begin{matrix}\dfrac{x}{x+y+z}\in N\\\dfrac{y}{y+x+t}\in N\\\dfrac{z}{z+t+y}\in N\\\dfrac{t}{t+z+x}\in N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x⋮x+y+z\\y⋮y+x+t\\z⋮z+t+y\\t⋮t+z+x\end{matrix}\right.\)
Vì \(x,y,z,t\in N\)*\(\Rightarrow x,y,z,t>0\)\(\Rightarrow\left\{{}\begin{matrix}x>x+y+z\\y>x+y+t\\z>y+z+t\\t>x+z+t\end{matrix}\right.\)(vô lí)
Vậy rõ ràng điều giả sử là vô lí. Nên \(M\notin N\left(đpcm\right)\)
Mình chỉ giúp đc đến đây thôi, mong bn thông cảm
Ngoài ra, chúc bn học tốt nhé
TM
20 tháng 10 2017
Bài toán 2.
Ta có: \(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+....+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(=\dfrac{2009-1}{1}+\dfrac{2009-2}{2}+\dfrac{2009-3}{3}+...+\dfrac{2009-2008}{2008}\)
\(=2009-1+\dfrac{2009}{2}-1+\dfrac{2009}{3}-1+....+\dfrac{2009}{2008}-1\)
\(=2009+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{....1}{2008}\right)-1.2008\)
\(=\left(2009-2008\right)+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=1+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2008}+\dfrac{1}{2009}\right)\)
=\(2009.A\)
Do đó, tỉ số \(\dfrac{A}{B}=\dfrac{A}{2009.A}=\dfrac{1}{2009}\)
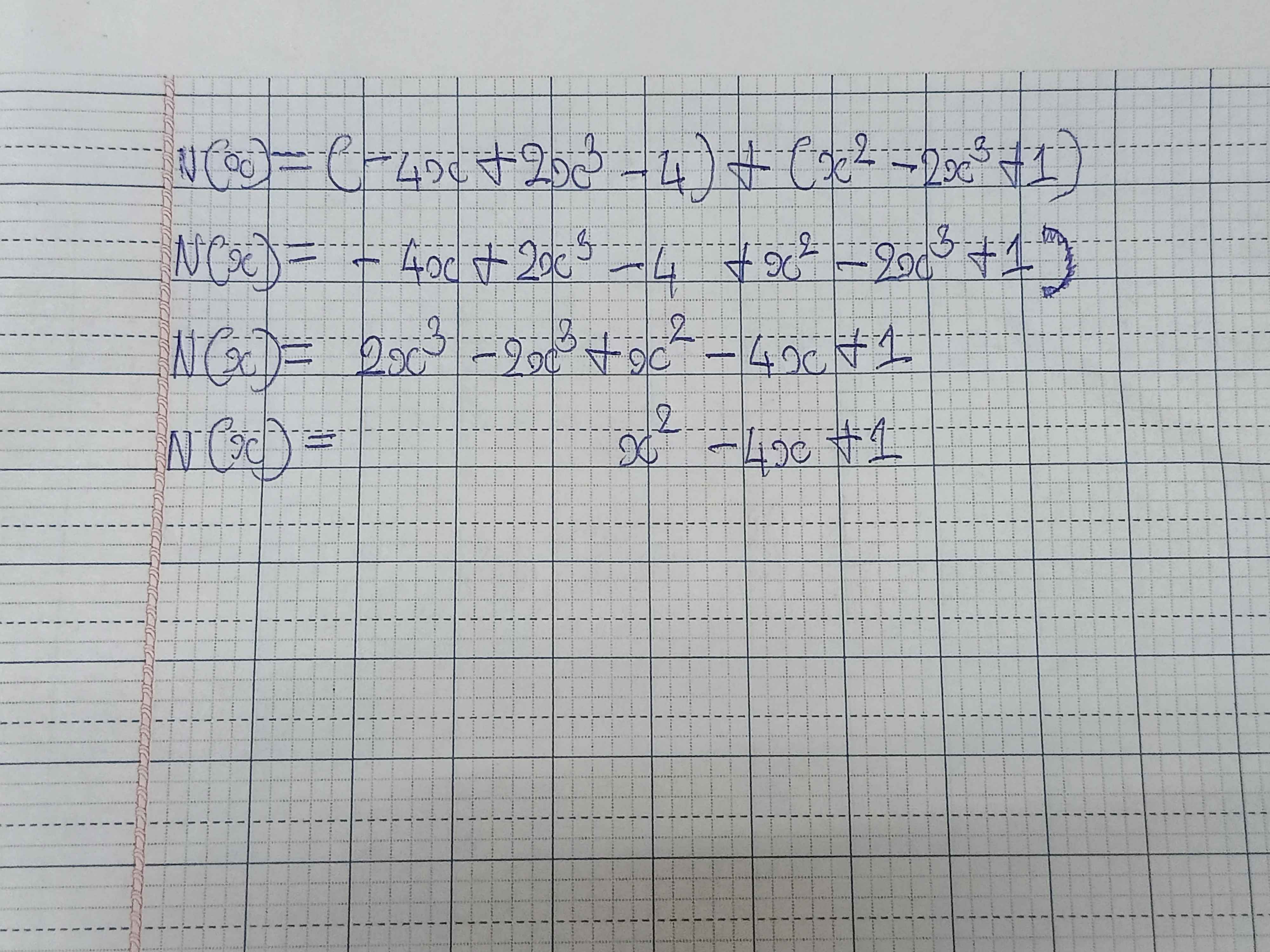
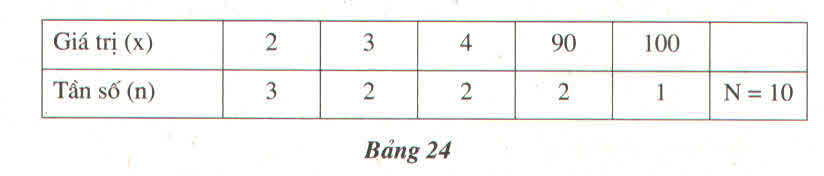
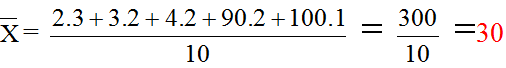
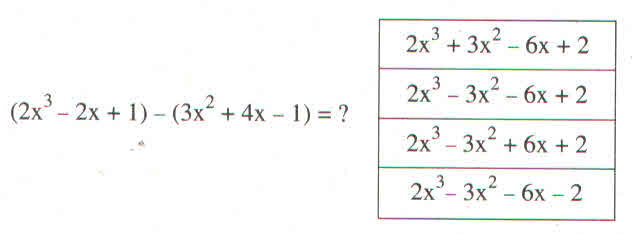
Có ai có câu trả lời chưa cho biết hay sai đi