Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Goi G là diem doi xung voi A qua M.
Cm dc AG=4+4=8,CG=BA=6,AB=CG=6 (ACGB là hbh)
Suy ra tg ACG vuong tai G (Pythagoras dao,6^2+8^2=10^2)
Suy ra goc AGC=90°
Suy ra goc MAB=90° (AB//CG).
đã chứng minh xong
_______HẾT_________
6 10 4 A B C L M
Gọi L là điểm đối xứng với A qua M.
Dễ dàng cm ABGC là hình bình hành \(\Rightarrow\)AB=CG=6 cm
Lại có AG=8 cm, áp dụng định lý Pitago đảo vào tam giác ACG, ta suy ra tam giác AGC vuông tại G(\(8^2+6^2=10^2\)
Lại có tam giac BAG= tam giác CGA . Do đó góc MAB= 90 độ

Cách 1: Gọi N là trung điểm của AC.
Xét tam giác ABC ta có:
M là trung điểm BC (gt)
N là trung điểm AC (cách vẽ)
=> MN là đường trung bình của tam giác ABC.
=> MN // AB và MN = 1/2 AB = 1/2 . 6 = 3 (cm)
Ta có:
AN = 1/2 AC ( N là trung điểm AC)
=> AN = 1/2 . 10 = 5 (cm)
Xét tam giác AMN ta có:
AN2 = 25 (cm)
AM2 + MN2 = 25 (cm)
=> AN2 = AM2 + MN2
=> Tam giác AMN vuông tại M ( Định lý Pitago đảo)
=> AM vuông góc với MN tại M
Mà MN // AB ( cmt)
Nên AB vuông góc với AM tại A
=> góc MAB = 90 độ ( đpcm)
Cách 2: Trên tia đối của tia MA lấy điểm E sao cho M là trung điểm của AE.
Xét tứ giác ABEC ta có:
2 đường chéo AE và BC cắt nhau tại M (gt)
M là trung điểm của BC (gt)
M là trung điểm của AE (cách vẽ)
=> Tứ giác ABEC là hình bình hành ( tứ giác có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
=> AB = EC = 6 cm.
Ta có:
AE = 2AM ( M là trung điểm của AE)
=> AE = 2 . 4 = 8 (cm)
Xét tam giác AEC ta có:
AC2 = 100 (cm)
AE2 + EC2 = 100 (cm)
=> AC2 = AE2 + EC2
=> Tam giác AEC vuông tại E.
=> góc AEC = 90 độ
Mà EC // AB ( tính chất hình bình hành ABEC)
Nên góc MAB = 90 độ ( đpcm)

A B C M 1 2 1 2
a) Xét \(\Delta AMC\) và \(\Delta AMB\) có:
AC = AB (gt)
CM = BM (gt,do M là trung điểm BC)
AM (cạnh chung)
Do đó \(\Delta AMC=\Delta AMB\) (c.c.c)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\Rightarrow\) M là tia phân giác của \(\widehat{BAC}\) (1)
b) \(\Delta AMC=\Delta AMB\) (chứng minh trên)
\(\Rightarrow\widehat{M_1}=\widehat{M_2}\). Mà \(\widehat{M_1} +\widehat{M_2}=180^o\) (kề bù)
Nên \(\widehat{M_1}=\widehat{M_2}=\frac{180^o}{2}=90^o\)
Suy ra \(AM\perp BC\) (2)
Từ (1) và (2) suy ra đpcm

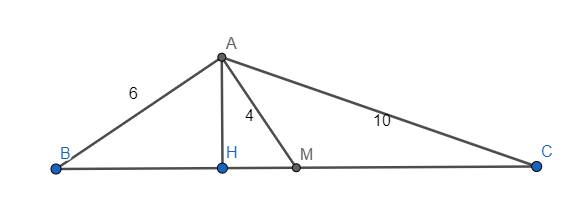
Hạ \(AH\perp BC\) tại H. Đặt \(MB=MC=x;HM=y;AH=h\)
Theo định lý Pythagoras: \(\left\{{}\begin{matrix}AH^2+HM^2=AM^2\\AH^2+BH^2=AB^2\\AH^2+CH^2=AC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+\left(x-y\right)^2=36\\h^2+\left(x+y\right)^2=100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+x^2+y^2-2xy=36\\h^2+x^2+y^2+2xy=100\end{matrix}\right.\)
Cộng theo vế của 2 pt thứ 2 và thứ 3 của hệ này, ta được:
\(2\left(h^2+x^2+y^2\right)=136\)
\(\Leftrightarrow x^2+\left(h^2+y^2\right)=68\)
\(\Leftrightarrow x^2+16=68\)
\(\Leftrightarrow x^2=52\) hay \(BM^2=52\)
Mà ta lại có \(AB^2+AM^2=6^2+4^2=52\)
\(\Rightarrow AB^2+AM^2=BM^2\) \(\Rightarrow\Delta ABM\) vuông tại A \(\Rightarrow\) đpcm
Gọi H là điểm đối xứng với A qua M
Xét tam giác AMB và tam giác HMC có:
\(\left\{{}\begin{matrix}HM=AM\\\widehat{AMB}=\widehat{HMC}\\MB=MC\end{matrix}\right.\)
\(\Rightarrow\Delta AMB=\Delta HMC\left(c.g.c\right)\)
\(\Rightarrow HC=AB=6cm\)
Xét tam giác HAC có:
\(AH^2+HC^2=10^2\left(8^2+6^2=10^2\right)\)
\(\Rightarrow\widehat{AHC}=90^o\)
Mà \(\Delta AMB=\Delta HMC\)
\(\Rightarrow\widehat{MAB}=\widehat{MHC}=90^o\left(đpcm\right)\)