
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sin^2\alpha+\cos^2\alpha=1\)
\(\Rightarrow\cos\alpha=\sqrt{1-\sin^2\alpha}=\sqrt{1-\frac{1}{4}}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}\)



4:
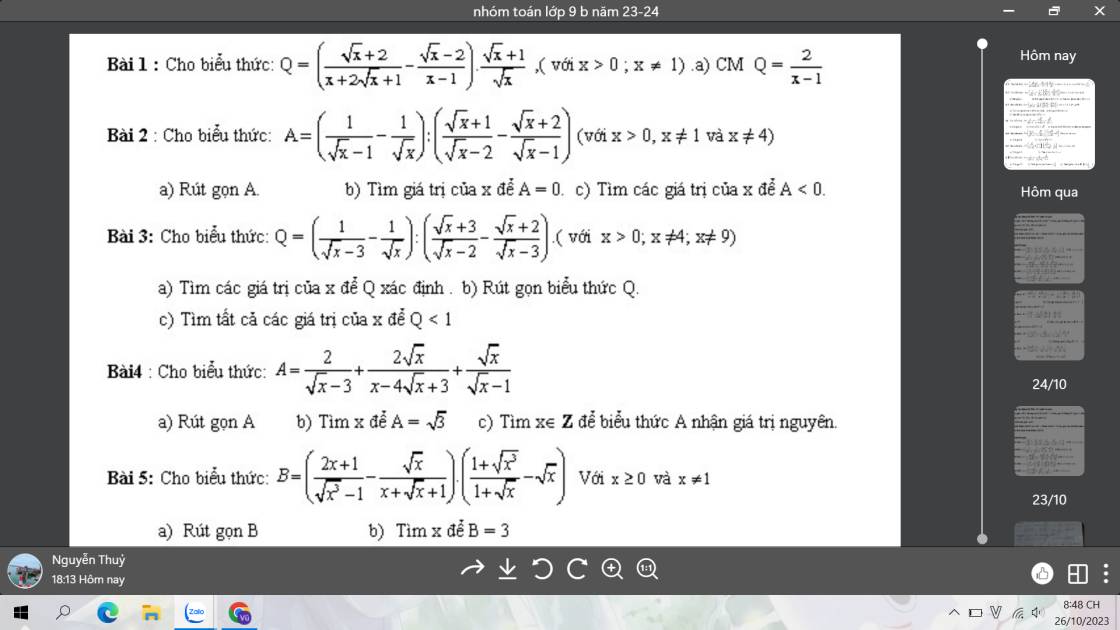
a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{1;9\right\}\end{matrix}\right.\)
\(A=\dfrac{2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{2\sqrt{x}-2+2\sqrt{x}+x-3\sqrt{x}}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b: A=căn 3
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}=\sqrt{3}\)
=>\(\sqrt{x}+2=\sqrt{3}\cdot\sqrt{x}-3\sqrt{3}\)
=>\(\sqrt{x}\left(1-\sqrt{3}\right)=-3\sqrt{3}-2\)
=>\(\sqrt{x}=\dfrac{3\sqrt{3}+2}{\sqrt{3}-1}=\dfrac{11+5\sqrt{3}}{2}\)
=>\(x=\dfrac{98+55\sqrt{3}}{2}\)
c: Để A nguyên thì \(\sqrt{x}-3+5⋮\sqrt{x}-3\)
=>\(\sqrt{x}-3\in\left\{1;-1;5;-5\right\}\)
=>\(\sqrt{x}\in\left\{4;2;8;-2\right\}\)
=>\(\sqrt{x}\in\left\{4;2;8\right\}\)
=>\(x\in\left\{16;4;64\right\}\)

Em mới vừa nghĩ ra cách khác )):
\(VT=\frac{a^2+b^2}{a^2b^2}+\frac{4}{a^2-2ab+b^2}=a^2+b^2+\frac{4}{a^2+b^2-2}\)
\(=a^2+b^2-2+\frac{4}{a^2+b^2-2}+2\)
\(\ge2\sqrt{\left(a^2+b^2-2\right).\frac{4}{a^2+b^2-2}}+2=6\)

Lời giải:
$2020\equiv 1\pmod 3\Rightarrow 2020x^3\equiv x^3\pmod 3$
$2021\equiv -1\pmod 3\Rightarrow 2021x\equiv -x\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv x^3-x\pmod 3$
Mà $x^3-x=x(x^2-1)=x(x-1)(x+1)$ là tích 3 số nguyên liên tiếp nên $x^3-x\equiv 0\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv 0\pmod 3(*)$
Mặt khác:
$y^{2022}=(y^{1011})^2$ là scp nên $y^{2022}\equiv 0,1\pmod 3$
$2023\equiv 1\pmod 3$
$\Rightarrow y^{2022}+2023\equiv 1,2\pmod 3(**)$
Từ $(*); (**)\Rightarrow 2020x^3+2021x\neq y^{2022}+2023$ với mọi $x,y$ nguyên.
Do đó không tồn tại $x,y$ thỏa đề.
Lời giải:
$2020\equiv 1\pmod 3\Rightarrow 2020x^3\equiv x^3\pmod 3$
$2021\equiv -1\pmod 3\Rightarrow 2021x\equiv -x\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv x^3-x\pmod 3$
Mà $x^3-x=x(x^2-1)=x(x-1)(x+1)$ là tích 3 số nguyên liên tiếp nên $x^3-x\equiv 0\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv 0\pmod 3(*)$
Mặt khác:
$y^{2022}=(y^{1011})^2$ là scp nên $y^{2022}\equiv 0,1\pmod 3$
$2023\equiv 1\pmod 3$
$\Rightarrow y^{2022}+2023\equiv 1,2\pmod 3(**)$
Từ $(*); (**)\Rightarrow 2020x^3+2021x\neq y^{2022}+2023$ với mọi $x,y$ nguyên.
Do đó không tồn tại $x,y$ thỏa đề.
Khi x=căn 3/4 thì \(M=\dfrac{1+\dfrac{\sqrt{3}}{2}}{1+\sqrt{1+\dfrac{\sqrt{3}}{2}}}+\dfrac{1-\dfrac{\sqrt{3}}{2}}{1-\sqrt{1-\dfrac{\sqrt{3}}{2}}}\)
\(=\dfrac{\sqrt{2}+\sqrt{6}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}+\dfrac{\sqrt{2}-\sqrt{6}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}\)
\(=\dfrac{2\sqrt{3}+2}{2+\sqrt{3}+1}+\dfrac{2-2\sqrt{3}}{2-\sqrt{3}+1}\)
\(=\dfrac{2\left(\sqrt{3}+1\right)}{\sqrt{3}\left(\sqrt{3}+1\right)}+\dfrac{2\left(1-\sqrt{3}\right)}{\sqrt{3}\left(\sqrt{3}-1\right)}=0\)