Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(E=2\sqrt{40\sqrt{12}}+3\sqrt{5\sqrt{48}}-2\sqrt{\sqrt{75}}-4\sqrt{15\sqrt{27}}.\)
\(=8\sqrt{5\sqrt{3}}+6\sqrt{5\sqrt{3}}-2\sqrt{5\sqrt{3}-12\sqrt{5\sqrt{3}}}\)
\(=0\)
b) \(F=\frac{1}{\sqrt{3}}+\frac{1}{3\sqrt{2}}+\frac{1}{\sqrt{3}}\sqrt{\frac{5}{12}-\frac{1}{\sqrt{6}}}.\)
Vì \(=\frac{5}{12}-\frac{1}{\sqrt{6}}=\frac{5-2\sqrt{6}}{12}=\frac{\left(\sqrt{3}-\sqrt{2}\right)^2}{12}\)
\(\frac{1}{\sqrt{3}}+\frac{1}{2\sqrt{3}}=\frac{\sqrt{3}}{3}+\frac{\sqrt{2}}{6}=\frac{2\sqrt{3}+\sqrt{2}}{6}\)
Nên \(F=\frac{2\sqrt{3}+\sqrt{2}}{6}+\frac{1}{\sqrt{3}}\sqrt{\frac{\left(\sqrt{3}-\sqrt{2}\right)^2}{12}}=\frac{2\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}}{6}=\frac{3\sqrt{3}}{6}=\frac{\sqrt{3}}{2}\)

a ) \(\dfrac{2}{\sqrt{3}-1}\) - \(\dfrac{2}{\sqrt{3}+1}\) = \(\dfrac{2\left(\sqrt{3}+1\right)-2\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
= \(\dfrac{2\sqrt{3}+2-2\sqrt{3}+2}{3-1}\) = \(\dfrac{4}{2}\) = 2
b) \(\dfrac{5}{12\left(2\sqrt{5}+3\sqrt{2}\right)}\) - \(\dfrac{5}{12\left(2\sqrt{5}-3\sqrt{2}\right)}\)
= \(\dfrac{5\left(2\sqrt{5}-3\sqrt{2}\right)-5\left(2\sqrt{5}+3\sqrt{2}\right)}{12\left(2\sqrt{5}+3\sqrt{2}\right)\left(2\sqrt{5}-3\sqrt{2}\right)}\)
= \(\dfrac{10\sqrt{5}-15\sqrt{2}-10\sqrt{5}-15\sqrt{2}}{12\left(20-18\right)}\)
= \(\dfrac{-30\sqrt{2}}{24}\) = \(\dfrac{-15\sqrt{2}}{12}\) = \(\dfrac{-5\sqrt{2}}{4}\)
c) \(\dfrac{5+\sqrt{5}}{5-\sqrt{5}}\) +\(\dfrac{5-\sqrt{5}}{5+\sqrt{5}}\) = \(\dfrac{\left(5+\sqrt{5}\right)^2+\left(5-\sqrt{5}\right)^2}{\left(5-\sqrt{5}\right)\left(5+\sqrt{5}\right)}\)
= \(\dfrac{25+10\sqrt{5}+5+25-10\sqrt{5}+5}{25-5}\) = \(\dfrac{60}{20}\) = 3
d) \(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3+1}}-1}\) - \(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3+1}}+1}\)
= \(\dfrac{\sqrt{3}}{\sqrt{2}-1}\) - \(\dfrac{\sqrt{3}}{\sqrt{2}+1}\) = \(\dfrac{\sqrt{3}\left(\sqrt{2}+1\right)-\sqrt{3}\left(\sqrt{2}-1\right)}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}\)
= \(\dfrac{\sqrt{6}+\sqrt{3}-\sqrt{6}+\sqrt{3}}{2-1}\) = \(2\sqrt{3}\)

1. C=\(\dfrac{1}{\sqrt{3}+\sqrt{2}}-\dfrac{\sqrt{15}-\sqrt{12}}{\sqrt{5}-2}\)
=\(\dfrac{1}{\sqrt{3}+\sqrt{2}}-\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{4}\right)}{\sqrt{5}-\sqrt{4}}=\dfrac{1}{\sqrt{3}+\sqrt{2}}-\sqrt{3}\)
=\(\dfrac{1-\sqrt{3}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}=\dfrac{1-3-\sqrt{6}}{\sqrt{3}+\sqrt{2}}=\dfrac{-2-\sqrt{6}}{\sqrt{3}+\sqrt{2}}=\dfrac{-\sqrt{2}\left(\sqrt{2}+\sqrt{3}\right)}{\sqrt{3}+\sqrt{2}}=-\sqrt{2}\)

Nhận xét: Cách làm thứ nhật (nhận dạng tử có thể phân tích thành nhân tử để rút gọn nhân tử đó với mẫu thích hợp hơn cách làm thứ hai (trục căn thức ở mẫu rồi thu gọn). Vì trục căn thức ở mẫu rồi rút gọn sẽ thêm nhiều phép nhân.
Nhận xét: Cách làm thứ nhật (nhận dạng tử có thể phân tích thành nhân tử để rút gọn nhân tử đó với mẫu thích hợp hơn cách làm thứ hai (trục căn thức ở mẫu rồi thu gọn). Vì trục căn thức ở mẫu rồi rút gọn sẽ thêm nhiều phép nhân.

\(A=\dfrac{\sqrt{15}-\sqrt{12}}{\sqrt{5}-2}-\dfrac{1}{2-\sqrt{3}}=\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{4}\right)}{\sqrt{5}-2}-\dfrac{2+\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{\sqrt{3}\left(\sqrt{5}-2\right)}{\sqrt{5}-2}-\dfrac{2+\sqrt{3}}{4-3}=\sqrt{3}-\left(2-\sqrt{3}\right)=\sqrt{3}-2-\sqrt{3}=-2\)
Vậy A=-2
căn ký hiệu là v nhé
v15=v3.v5; v12= 2.v3 thay vào có:
A = v3 - 1/(2-v3) = (2v3-3-1)/(2-v3)
= 2(v3-2) / (2-v3) = -2

a. \(\sqrt{8-2\sqrt{15}}-\sqrt{8+2\sqrt{15}}\)
= \(\sqrt{3-2\sqrt{15}+5}-\sqrt{3+2\sqrt{15}+5}\)
= \(\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{3}+\sqrt{5}\right)^2}\)
= \(\sqrt{5}-\sqrt{3}-\sqrt{3}-\sqrt{5}\)
= \(-2\sqrt{3}\)
b. \(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\dfrac{5-2\sqrt{5}}{2\sqrt{5}-4}\)
= \(\dfrac{\left(\sqrt{15}-\sqrt{5}\right).\left(\sqrt{3}+1\right)}{2}+\dfrac{\left(5-2\sqrt{5}\right).\left(2\sqrt{5}+4\right)}{4}\)
=\(\dfrac{\sqrt{45}+\sqrt{15}-\sqrt{15}-\sqrt{5}}{2}+\dfrac{\left(5-2\sqrt{5}\right).2\left(\sqrt{5}+2\right)}{4}\)
= \(\dfrac{3\sqrt{5}-\sqrt{5}}{2}+\dfrac{\left(5-2\sqrt{5}\right).\left(\sqrt{5}+2\right)}{2}\)
= \(\dfrac{2\sqrt{5}}{2}+\dfrac{5\sqrt{5}+10-10-4\sqrt{5}}{2}\)
= \(\sqrt{5}+\dfrac{\sqrt{5}}{2}\)
= \(\dfrac{3\sqrt{5}}{2}\)
c. \(\left(\dfrac{1}{\sqrt{5}-\sqrt{2}}+\dfrac{1}{\sqrt{5}+\sqrt{2}}\right):\dfrac{1}{\left(\sqrt{2}+1\right)^2}\)
= \(\dfrac{\sqrt{5}+\sqrt{2}+\sqrt{5}-\sqrt{2}}{\left(\sqrt{5}-\sqrt{2}\right).\left(\sqrt{5}+\sqrt{2}\right)}.\left(\sqrt{2}+1\right)^2\)
= \(\dfrac{2\sqrt{5}}{3}.\left(2+2\sqrt{2}+1\right)\)
= \(\dfrac{2\sqrt{5}}{3}.\left(3+2\sqrt{2}\right)\)
= \(\dfrac{6\sqrt{5}+4\sqrt{10}}{3}\)
d. \(\left(\dfrac{2}{\sqrt{3}-1}+\dfrac{3}{\sqrt{3}-2}+\dfrac{15}{3-\sqrt{3}}\right).\dfrac{1}{\sqrt{3}+5}\)
= \(\left(\sqrt{3}+1-3\left(\sqrt{3}+2\right)+\dfrac{5\left(3+\sqrt{3}\right)}{2}\right).\dfrac{1}{\sqrt{3}+5}\)
= \(\left(\sqrt{3}+1-6-3\sqrt{3}+\dfrac{15+5\sqrt{3}}{2}\right).\dfrac{1}{\sqrt{3}+5}\)
= \(\left(-2\sqrt{3}-5+\dfrac{15+5\sqrt{3}}{2}\right).\dfrac{1}{\sqrt{3}+5}\)
= \(\dfrac{-4\sqrt{3}-10+15+5\sqrt{3}}{2}.\dfrac{1}{\sqrt{3}+5}\)
= \(\dfrac{\sqrt{3}+5}{2}.\dfrac{1}{\sqrt{3}+5}\)
= \(\dfrac{1}{2}\)
Nếu đúng cho 1 like nhé!

\(A=\frac{1}{\sqrt{1}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{5}}+...+\frac{1}{\sqrt{23}+\sqrt{25}}\)
\(2A=\frac{2}{\sqrt{3}+\sqrt{1}}+\frac{2}{\sqrt{5}+\sqrt{3}}+...+\frac{2}{\sqrt{25}+\sqrt{23}}\)\(2A=\frac{2\left(\sqrt{3}-\sqrt{1}\right)}{\left(\sqrt{3}+\sqrt{1}\right)\left(\sqrt{3}-\sqrt{1}\right)}+\frac{2\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}+...+\frac{2\left(\sqrt{25}-\sqrt{23}\right)}{\left(\sqrt{25}+\sqrt{23}\right)\left(\sqrt{25}-\sqrt{23}\right)}\)
\(2A=\frac{2\left(\sqrt{3}-\sqrt{1}\right)}{2}+\frac{2\left(\sqrt{5}-\sqrt{3}\right)}{2}+...+\frac{2\left(\sqrt{25}-\sqrt{23}\right)}{2}\)
\(2A=\sqrt{3}-\sqrt{1}+\sqrt{5}-\sqrt{3}+\sqrt{25}-\sqrt{23}\)
\(2A=\sqrt{25}-\sqrt{1}\)
\(2A=4\)
\(A=2\)

\(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}=\dfrac{\left(2+\sqrt{2}\right)\left(\sqrt{2}-1\right)}{2-1}=2\sqrt{2}-2+2-\sqrt{2}=\sqrt{2}\)
\(\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}=-\sqrt{5}\)
\(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{2}\)
\(\dfrac{a-\sqrt{a}}{1-\sqrt{a}}=\dfrac{\left(a-\sqrt{a}\right)\left(1+\sqrt{a}\right)}{1-a}=\dfrac{a+a\sqrt{a}-\sqrt{a}-a}{1-a}=\dfrac{\sqrt{a}\left(a-1\right)}{1-a}=-\sqrt{a}\)
\(\dfrac{p-2\sqrt{p}}{\sqrt{p}-2}=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)
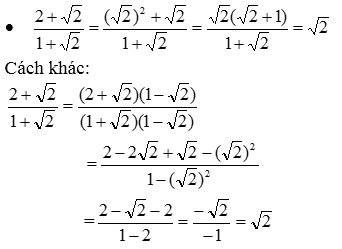
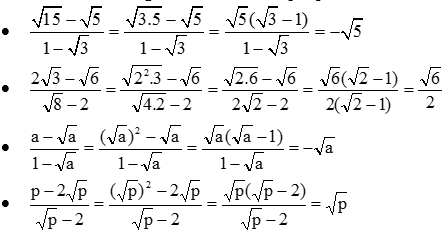

\(A=\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)}-\dfrac{\sqrt{3}\left(\sqrt{5}-2\right)}{\sqrt{5}-2}\)
\(=\dfrac{\sqrt{3}-\sqrt{2}}{3-2}-\sqrt{3}=\sqrt{3}-\sqrt{2}-\sqrt{3}\)
\(=-\sqrt{2}\)