Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tại mọi điểm \(x\ne1\) hàm đã cho là hàm đa thức nên liên tục
Xét tại \(x=1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(3x+2\right)=5\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(x^2-1\right)=0\)
Do \(\lim\limits_{x\rightarrow1^+}f\left(x\right)\ne\lim\limits_{x\rightarrow1^-}f\left(x\right)\) nên hàm số đã cho ko liên tục tại \(x=1\)

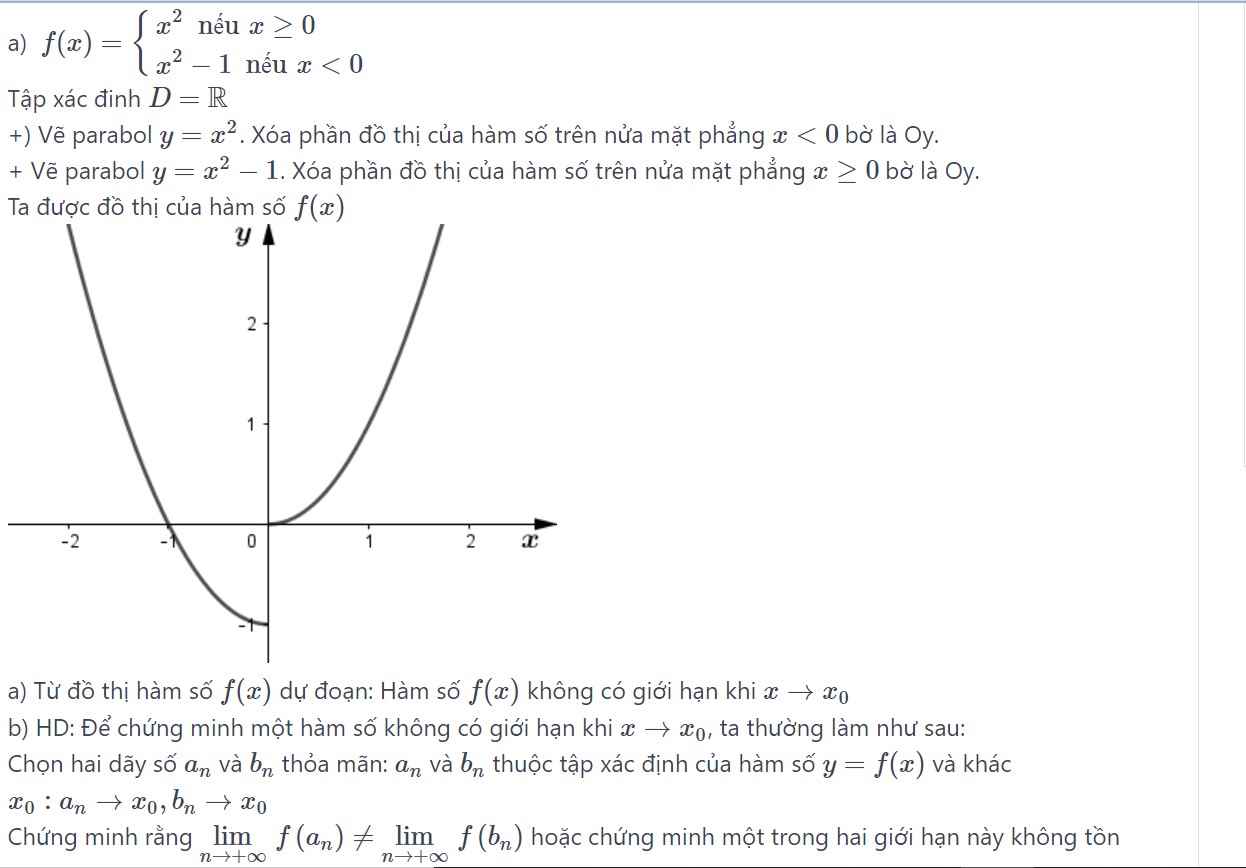
a) Các bạn tự vẽ hình nhé . Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 – 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có =![]() = 3(-1) +2 = -1.
= 3(-1) +2 = -1.
![]() = (-1)2 – 1 = 0.
= (-1)2 – 1 = 0.
Vì ![]() nên không tồn tại
nên không tồn tại  . Vậy hàm số gián đoạn tại
. Vậy hàm số gián đoạn tại
x0 = -1.
TenAnh1 TenAnh1 A = (-0.04, -7.12) A = (-0.04, -7.12) A = (-0.04, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) D = (10.58, -5.6) D = (10.58, -5.6) D = (10.58, -5.6)

a) f(x) liên tục tại x0 = -2
Vì \(\lim\limits_{x\rightarrow-2}f\left(x\right)=f\left(-2\right)=25\)
b) Có: \(\lim\limits_{x\rightarrow\frac{1}{2}}f\left(x\right)=\lim\limits_{x\rightarrow\frac{1}{2}}\frac{\left(2x-1\right)\left(2x+1\right)}{2x-1}=\lim\limits_{x\rightarrow\frac{1}{2}}\left(2x+1\right)=2\)
mà \(f\left(\frac{1}{2}\right)=3\)
=> \(\lim\limits_{x\rightarrow\frac{1}{2}}f\left(x\right)\ne f\left(\frac{1}{2}\right)\)
=> f(x) gián đoạn tại x0 = 1/2
c) \(\lim\limits_{x\rightarrow2-}f\left(x\right)=\lim\limits_{x\rightarrow2-}=\lim\limits_{x\rightarrow2-}\left(2x^2+x-1\right)=9\)
\(f\left(2\right)=3.2-5=1\)
Vì \(\lim\limits_{x\rightarrow2-}f\left(x\right)\ne f\left(2\right)\)
nên f(x) gián đoạn tại x0 = 2

Bạn viết lại đề được ko? Ko hiểu \(\frac{x'+x}{x}\) với \(x\ne0\) là gì
Các câu dưới cũng có kí hiệu này, chắc bạn viết nhầm sang kí hiệu nào đó, nó cũng ko phải kí hiệu đạo hàm

\(\lim\limits_{x\rightarrow0}\left|f\left(x\right)\right|=\lim\limits_{x\rightarrow0}\left|x^2sin\dfrac{1}{x}\right|< \lim\limits_{x\rightarrow0}\left|x^2\right|=0\).
Vậy \(\lim\limits_{x\rightarrow0}f\left(x\right)=0\).
\(f\left(0\right)=A\).
Để hàm số liên tục tại \(x=0\) thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\Leftrightarrow A=0\).
Để xét hàm số có đạo hàm tại \(x=0\) ta xét giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0}\dfrac{x^2sin\dfrac{1}{x}}{x}=\lim\limits_{x\rightarrow0}xsin\dfrac{1}{x}=0\).
Vậy hàm số có đạo hàm tại \(x=0\).

Hàm số liên tục tại mọi điểm khác 0 và 2
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2x+1\right)=1\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\left(x-1\right)^3=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow0^-}f\left(x\right)\ne\lim\limits_{x\rightarrow0^+}f\left(x\right)\)
\(\Rightarrow f\left(x\right)\) gián đoạn tại \(x_0=0\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(x-1\right)^3=1\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(\sqrt{x}-1\right)=\sqrt{2}-1\)
\(\Rightarrow\lim\limits_{x\rightarrow2^-}f\left(x\right)\ne\lim\limits_{x\rightarrow2^+}f\left(x\right)\Rightarrow\) hàm số gián đoạn tại \(x_0=2\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}x^2+3x+1=1+3\cdot1+1=5\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}2x+2=2\cdot1+2=4\)
f(1)=1+3+1=5
=>\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)\ne\lim\limits_{x\rightarrow1^-}f\left(x\right)\)
=>Hàm số bị gián đoạn tại x=1