Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

để pt có 2 nghiệm đều âm thì denta >=0
S<0
p>0
denta=(-1)2 -4(m2+m-6)>=0 <=>1-4m2 -4m+24>=0
<=>-4m2-4m+25>=0 (tm)
s=1<0 (vô lí)
p=m2 +m-6 >0 m>2(tm)
vậy không có gtrij nào của m đề pt có 2 nghiệm dều âm

Ta có: \(a-b+c=1+2m-2m-1=0\)
Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=-1\\x_2=2m+1\end{matrix}\right.\)
Để biểu thức bài toán xác định thì:
\(\left\{{}\begin{matrix}x_1+x_2=2m\ge0\\3+x_1x_2=2-2m\ge0\end{matrix}\right.\) \(\Rightarrow0\le m\le1\)
\(\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1\)
\(\Leftrightarrow\sqrt{2m}+\sqrt{2-2m}=2m+1\)
\(\Leftrightarrow2m-\sqrt{2m}+1-\sqrt{2-2m}=0\)
\(\Leftrightarrow\frac{4m^2-2m}{2m+\sqrt{2m}}+\frac{2m-1}{1+\sqrt{2-2m}}=0\)
\(\Leftrightarrow\left(2m-1\right)\left(\frac{2m}{2m+\sqrt{2m}}+\frac{1}{1+\sqrt{2-2m}}\right)=0\)
\(\Leftrightarrow2m-1=0\Rightarrow m=\frac{1}{2}\)

Δ= 4m^2 - 4m^2 + 4m + 24 = 4m + 24
để pt có 2 nghiệm thì Δ ≥ 0 => 4m + 24 ≥ 0 <=> m ≥ -6
viet: \(\left\{{}\begin{matrix}x1+x2=2m\\x1\cdot x2=m^2-m+6\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}\left(x1+x2\right)^2=4m^2\\2x1\cdot x2=2m^2-2m+12\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x1^2+x2^2=4m^2-2x1\cdot x2\\2x1\cdot x2=2m^2-2m+12\end{matrix}\right.\)
|x1| + |x2| = 8
<=> (|x1| + |x2|)^2 = 64
<=> x1^2 + x2^2 + 2|x1|*|x2| = 64
<=> 4m^2 - 2m^2+2m-12 + 2m^2-2m+12 = 64
<=> 4m^2 = 64
<=> m = -4; m = 4

a) -5x2 + 3x + 2 = 0 (a = -5; b = 3; c = 2)
\(\Delta=3^2-4\cdot\left(-5\right)+2=31\)
=> Phương trình có nghiệm
Ta có a + b + c = -5 +3 +2 = 0
Nên phương trình có 2 nghiệm:
x1= 1; x2 = \(\dfrac{c}{a}\) = \(\dfrac{2}{-5}\) = \(\dfrac{-2}{5}\)
b) 7x2 + 6x - 13 = 0 (a = 7; b = 6; c = -13)
\(\Delta=6^2-4\cdot7\cdot\left(-13\right)=400\)
Nên phương trình có nghiệm
Ta có a + b + c = 7 + 6 +(-13) = 0
Nên phương trình có 2 nghiệm:
x1= 1; x2 = \(\dfrac{c}{a}=\dfrac{-13}{7}\)
c) x2 - 7x + 12 = 0 (a = 1; b = -7; c = 12)
\(\Delta\) = (-7)2 - 4 * 1 * 12= 1
Nên phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-7\right)+\sqrt{1}}{2\cdot1}=4\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-7\right)-\sqrt{1}}{2\cdot1}=3\)
Vậy phương trình có 2 nghiệm x1=4 và x2=3
d)-0,4x2 +0,3x +0,7 =0 (a = -0,4; b= 0,3; c= 0,7)
\(\Delta=\left(0,3\right)^2-4\cdot\left(-0,4\right)\cdot0,3=0,57\)
Nên phương trình có nghiệm
Ta có a - b + c = (-0,4) - 0,3 + 0,7 = 0
Nên phương trình có 2 nghiệm x1 = -1; \(x_2=\dfrac{-c}{a}=\dfrac{-0,7}{-0,4}=\dfrac{7}{4}\)
e)3x2+(3-2m)x-2m =0(a= 3;b=3-2m;c= -2m)
\(\Delta=\left(3-2m\right)^2-4\cdot3\cdot\left(-2m\right)\)
= 9 - 12m + 4m +24m = 9 + 16m
Do \(\left\{{}\begin{matrix}9>0\\16m\ge0\end{matrix}\right.\)nên phương trình có nghiệm
Ta có a - b + c = 3- (3-2m) +( -2m)
= 3 -3 + 2m - 2m = 0
Nên phương trình có 2 nghiệm
x1= - 1; x2=\(\dfrac{-c}{a}=\dfrac{-\left(-2m\right)}{3}=\dfrac{2m}{3}\)
f) 3x2 - \(\sqrt{3}\)x - ( 3+\(\sqrt{3}\))=0
(a= 3; b= \(-\sqrt{3}\); c=\(-\left(3+\sqrt{3}\right)\))
\(\Delta=\left(-\sqrt{3}\right)^2-4\cdot3\cdot\left(-\left(3+\sqrt{3}\right)\right)\)
= 39+12\(\sqrt{3}\)
Nên phương trình có nghiệm
Ta có a - b +c = 3 - (\(-\sqrt{3}\)) + (-(3+\(\sqrt{3}\))) = 0
Phương trình có 2 nghiệm x1= -1;
x2=\(\dfrac{-c}{a}=\dfrac{-\left(-\left(3+\sqrt{3}\right)\right)}{3}=\dfrac{3+\sqrt{3}}{3}\)

a: TH1: m=-1
Pt trở thành \(-3x-2\cdot\left(-1\right)-1=0\)
=>-3x+1=0
hay x=1/3(nhận)
Th2: m<>-1
\(\text{Δ}=\left(3m\right)^2-4\left(m+1\right)\left(-2m-1\right)\)
\(=9m^2+\left(4m+4\right)\left(2m+1\right)\)
\(=9m^2+8m^2+4m+8m+4\)
\(=17m^2+12m+4\)
Đặt \(17m^2+12m+4=0\)
\(\text{Δ}=12^2-4\cdot17\cdot4=-128< 0\)
Do đó: Phương trình vô nghiệm
b:
TH2: m<>1/2
\(\text{Δ}=\left(-m\right)^2+4\left(m+1\right)\left(2m-1\right)\)
\(=m^2+\left(4m+4\right)\left(2m-1\right)\)
\(=m^2+8m^2-4m+8m-4\)
\(=9m^2+4m-4\)
Đặt \(9m^2+4m-4=0\)
\(\text{Δ}=4^2-4\cdot9\cdot\left(-4\right)=160>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{-4-4\sqrt{10}}{18}=\dfrac{-2-\sqrt{10}}{9}\left(loại\right)\\m_2=\dfrac{\sqrt{10}-2}{9}\left(nhận\right)\end{matrix}\right.\)
Do đó: Phương trình (1) có hai nghiệm phân biệt

Bài 2:
Để pt có 2 nghiệm phân biệt thì:
$\Delta=9-4m>0\Leftrightarrow m< \frac{9}{4}$
Áp dụng định lý Viet với 2 nghiệm $x_1,x_2$: \(\left\{\begin{matrix} x_1+x_2=3\\ x_1x_2=m\end{matrix}\right.\)
Khi đó:
\(\sqrt{x_1^2+1}+\sqrt{x_2^2+1}=3\sqrt{3}\)
\(\Leftrightarrow x_1^2+x_2^2+2+2\sqrt{(x_1^2+1)(x_2^2+1)}=27\)
\(\Leftrightarrow (x_1+x_2)^2-2x_1x_2+2+2\sqrt{(x_1x_2)^2+(x_1^2+x_2^2)+1}=27\)
\(\Leftrightarrow (x_1+x_2)^2-2x_1x_2+2+2\sqrt{(x_1x_2)^2+(x_1+x_2)^2-2x_1x_2+1}=27\)
$\Leftrightarrow 9-2m+2+2\sqrt{m^2+9-2m+1}=27$
$\Leftrightarrow \sqrt{m^2-2m+10}=m+8$
\(\Rightarrow \left\{\begin{matrix} m\geq -8\\ m^2-2m+10=(m+8)^2=m^2+16m+64\end{matrix}\right.\)
\(\Rightarrow m=-3\) (thỏa mãn)
Vậy........
Bài 1:
Ta thấy $\Delta'=m^2-(m^2-2)=2>0$ với mọi $m$ nên PT có 2 nghiệm phân biệt với mọi $m$
Áp dụng định lý Viet, với $x_1,x_2$ là nghiệm của pt thì:
\(\left\{\begin{matrix} x_1+x_2=2m\\ x_1x_2=m^2-2\end{matrix}\right.\)
Khi đó:
\(|x_1^3-x_2^3|=10\sqrt{2}\)
\(\Leftrightarrow |x_1-x_2||x_1^2+x_1x_2+x_2^2|=10\sqrt{2}\)
\(\Leftrightarrow \sqrt{(x_1+x_2)^2-4x_1x_2}.|(x_1+x_2)^2-x_1x_2|=10\sqrt{2}\)
\(\Leftrightarrow \sqrt{4m^2-4(m^2-2)}.|4m^2-(m^2-2)|=10\sqrt{2}\)
\(\Leftrightarrow |3m^2+2|=5\Leftrightarrow 3m^2+2=5\Leftrightarrow m=\pm 1\) (thỏa mãn)
Vậy........

b) Để phương trình có nghiệm thì \(\Delta'=\left(-m\right)^2-\left(m-1\right)\ge0\Leftrightarrow m^2-m+1\ge0\)
Điều này hiển nhiên vì \(m^2-m+1=\left(m-\frac{1}{2}\right)^2+\frac{3}{4}>0\forall m\)
Theo đề bài suy ra \(x_1+x_2+2\sqrt{x_1x_2}=4\) (bình phương hai vế của giả thiết)
Chị thay tiếp vô hệ thức Viet và em không chắc.
Xét \(\Delta^,=\left(-m\right)^2-\left(m-1\right)\)\(=m^2-m+1\)
\(=(m^2-2\cdot m\cdot\frac{1}{2}+\frac{1}{4})+\frac{3}{4}\)\(=\left(m-\frac{1}{2}\right)^2+\frac{3}{4}>0\)với mọi m
Theo Vi- ét :\(\hept{\begin{cases}x_1+x_2=2m\\x_1\cdot x_2=m-1\end{cases}}\)(1)
Theo bài ra ta có : \(\sqrt{x_1}+\sqrt{x_2}=2\)
\(\Leftrightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=4\)\(\Leftrightarrow x_1+2\sqrt{x_1\cdot x_2}+x_2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)+2\sqrt{x_1\cdot x_2}=4\)(*)
Thay (1) vào (*) ta được :
\(2m+2\sqrt{m-1}=4\)\(\Leftrightarrow2\sqrt{m-1}=4-2m\)
\(\Leftrightarrow\sqrt{m-1}=2-m\)\(\Leftrightarrow\sqrt{m-1}^2=\left(2-m\right)^2\)
\(\Leftrightarrow|m-1|=4-4m+m^2\)
\(\Leftrightarrow\orbr{\begin{cases}m-1=4-4m+m^2\\m-1=-4+4m-m^2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}m^2-5m+5=0\left(2\right)\\m^2-3m+3=0\left(3\right)\end{cases}}\)
\(\Delta_{\left(2\right)}=\left(-5\right)^2-4\cdot5=5>0\)
=> Phương trình có 2 nghiệm phân biệt
\(m_1=\frac{5+\sqrt{5}}{2};m_2=\frac{5-\sqrt{5}}{2}\)
\(\Delta_{\left(3\right)}=\left(-3\right)^2-4\cdot3=-3< 0\)
=> phương trình vô nghiệm
KL : ....
kb vs mk nha
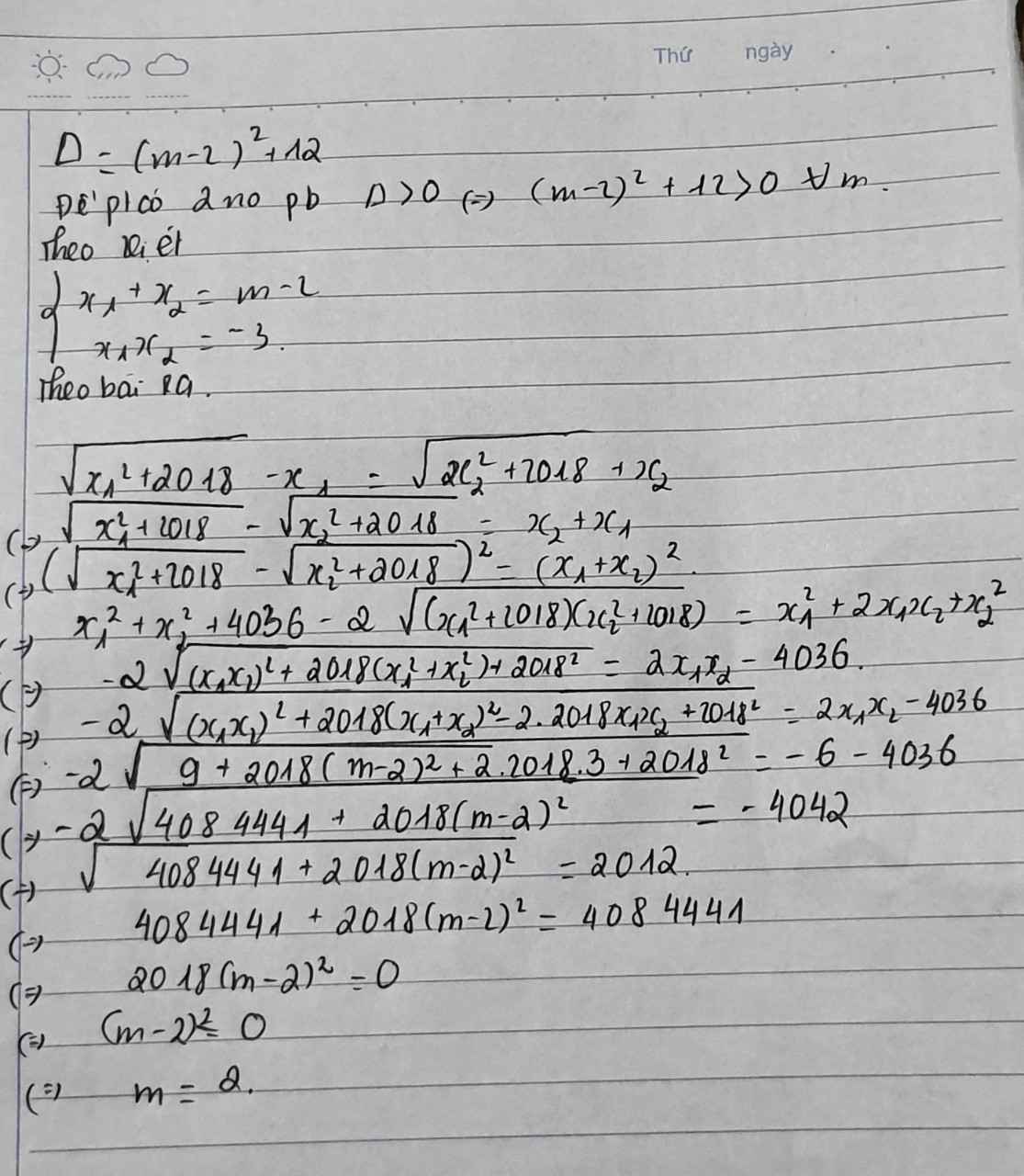
PT nhận \(x=1\) là nghiệm
Thay \(x=1\) vào trong PT ta tìm được m:
\(x^2-2mx+2m^2-m-6=0\)
\(\Rightarrow1^2-2\cdot m\cdot1+2m^2-m-6=0\)
\(\Leftrightarrow1-2m+2m^2-m-6=0\)
\(\Leftrightarrow2m^2-3m-5=0\)
\(\Leftrightarrow2m^2+2m-5m-5=0\)
\(\Leftrightarrow2m\left(m+1\right)-5\left(m+1\right)=0\)
\(\Leftrightarrow\left(m+1\right)\left(2m-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m+1=0\\2m-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=\dfrac{5}{2}\end{matrix}\right.\)
Vậy PT nhận \(x=1\) là nghiệm khi \(m=-1\) hoặc \(m=\dfrac{5}{2}\)
Thay \(x=1\) vào pt \(x^2-2mx+2m^2-m-6=0\)
\(\Rightarrow1^2-2m.1+2m^2-m-6=0\)
\(\Rightarrow-3m+2m^2-5=0\)
\(\Rightarrow2m^2-3m-5=0\)
\(\Delta=b^2-4ac=\left(-3\right)^2-4.2.\left(-5\right)=49>0\)
\(\Rightarrow\) Pt có 2 nghiệm \(m_1,m_2\)
\(\left\{{}\begin{matrix}m_1=\dfrac{3+\sqrt{49}}{2.2}=\dfrac{5}{2}\\m_2=\dfrac{3-\sqrt{49}}{2.2}=-1\end{matrix}\right.\)
Vậy \(m=\dfrac{5}{2},m=-1\) thì pt có 1 nghiệm \(x=1\)