


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



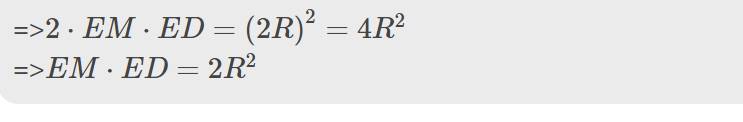

a: Xét ΔOEA vuông tại E có EM là đường cao
nên \(OM\cdot OA=OE^2\)
=>\(OA=\dfrac{10^2}{6}=\dfrac{50}{3}\left(cm\right)\)
ΔOEA vuông tại E
=>\(OE^2+EA^2=OA^2\)
=>\(EA^2+10^2=\left(\dfrac{50}{3}\right)^2\)
=>\(EA^2=\left(\dfrac{40}{3}\right)^2\)
=>EA=40/3(cm)
Xét ΔEAO vuông tại E có EM là đường cao
nên \(EM\cdot OA=EA\cdot EO\)
=>\(EM\cdot\dfrac{50}{3}=10\cdot\dfrac{40}{3}\)
=>\(EM\cdot50=10\cdot40\)
=>EM=400/50=8(cm)
Ta có: ΔOEF cân tại O
mà OM là đường cao
nên M là trung điểm của EF và OM là phân giác của góc EOF
=>\(EF=2\cdot EM=16\left(cm\right)\)
b: Xét ΔOEA và ΔOFA có
OE=OF
\(\widehat{EOA}=\widehat{FOA}\)
OA chung
Do đó: ΔOEA=ΔOFA
=>\(\widehat{OEA}=\widehat{OFA}=90^0\)
=>AFlà tiếp tuyến của (O)
c: Xét (O) có
ΔEFC nội tiếp
EC là đường kính
Do đó: ΔEFC vuông tại F
=>EF\(\perp\)FC tại F
=>CF\(\perp\)ED tại F
Xét ΔECD vuông tại C có EF là đường cao
nên \(EF\cdot ED=EC^2\)
=>\(2\cdot EM\cdot ED=\left(2R\right)^2=4R^2\)
=>\(EM\cdot ED=2R^2\)

a) Xét tứ giác AEOF có
\(\widehat{AEO}\) và \(\widehat{AFO}\) là hai góc đối
\(\widehat{AEO}+\widehat{AFO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEOF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

d, Vi ED la tiep tuyen (chung minh tren) => tam giac EDF vuong tai D
co \(\widehat{CDE}=\frac{1}{2}sd\widebat{DC}=\frac{1}{2}\widehat{COD}=\frac{1}{2}.120=60^o\)
ma \(\widehat{CED}+\widehat{COD}=180^o\Rightarrow\widehat{CED}=180-120=60^o\)
suy ra \(\Delta CED\) deu => EC=CD (1)
mat khac cung co \(\widehat{CFD}=\widehat{CDF}\) (phu hai goc bang nhau)
=> tam giac CDF can tai C
suy ra CD=CF (2)
tu (1),(2) suy ra dpcm