Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Các bức xạ đều cho vân sáng bậc k = 0 tại tại O ⇒vân trung tâm O là một vân trùng. Tại điểm M ≠O trên màn vân sáng của hai bức xạ trùng nhau thì ta có OM = k 1 i 1 = k 2 i 2 ( k 1 , k 2 nguyên dương)
⇒ k 1 λ 1 = k 2 λ 2 ⇒ k 1 k 2 = λ 2 λ 1 = 5 6 ⇒ k 1 chia hết cho 5, k 2 chia hết cho 6.
Vân trùng gần vân trung tâm nhất cách vân trung tâm một khoảng
i’ = k 1 min . i 1 = 5. λ 1 D a = 6 m m , các vân trùng nằm phân bố đều đặn trên màn và khoảng cách giữa hai vân trùng liên tiếp bằng i’= 6 mm.
Ta có L 2. i ' = 2 , 33
→ số vân trùng của hai bức xạ trên màn bằng n = 2 L 2 i ' + 1 = 2.2 + 1 = 5 vân.

Các bức xạ đều cho vân sáng bậc k = 0 tại tại O ⇒ vân trung tâm O là một vân trùng. Tại điểm M ≠ O trên màn vân sáng của hai bức xạ trùng nhau thì ta có
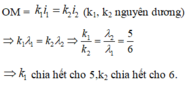
Vân trùng gần vân trung tâm nhất cách vân trung tâm một khoảng
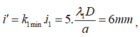
các vân trùng nằm phân bố đều đặn trên màn và khoảng cách giữa hai vân trùng liên tiếp bằng i’= 6 mm
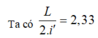
→ số vân trùng của hai bức xạ trên màn bằng
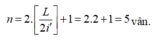
Đáp án A

Phương pháp: Sử dụng lí thuyết về giao thoa ánh sáng
Cách giải:
Đáp án B
- Vị trí trùng nhau của 3 bức xạ:
![]()
![]()
![]()
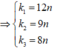
Trong khoảng giữa hai vân sáng cùng màu với vân trung tâm có 11 vân sáng của bức xạ 1; 8 vân sáng của bức xạ 2 và 7 vân sáng của bức xạ 3.
- Số vân sáng trùng nhau của λ 1 v à λ 2 :
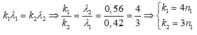
=> Trong khoảng giữa hai vân sáng liên tiếp có màu giống vân trung tâm có 2 vân trùng nhau của λ1 và λ2 (ứng với n1 = 1; 2)
- Số vân sáng trùng nhau của λ 1 v à λ 3 :
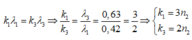
=> Trong khoảng giữa hai vân sáng liên tiếp có màu giống vân trung tâm có 3 vân trùng nhau của λ1 và λ2 (ứng với n2 = 1; 2; 3)
- Số vân sáng trùng nhau của λ 2 v à λ 3 :
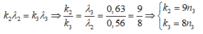
=> Trong khoảng giữa hai vân sáng liên tiếp có màu giống vân trung tâm không có vân trùng nhau của λ2 và λ3
- Vân sáng của hai bức xạ trùng nhau ta chỉ tính là 1 => Số vân sáng quan sát được:
N = 11 + 8 + 7 – 5 = 21

Đáp án: A
+ Điều kiện vân sáng của λ1 trùng với vân sáng của λ2:
k2/k1 = λ1/λ2 = 0,42/0,56 = a/b = 3/4
+) Điều kiện vân sáng của λ1 trùng với vân sáng của λ3:
k3/k1 = λ1/λ3 = 0,42/0,63 = c/d = 2/3
+) Điều kiện vân sáng của λ2 trùng với vân sáng của λ3:
k3/k2 = λ2/λ3 = 0,56/0,63 = e/f = 8/9
→ Khoảng vân trùng i = b.d.λ1 = a.d.λ2 = b.c.λ3
hay i = 12λ1 = 9λ2 = 8λ3
Trong khoảng giữa hai vân sáng liên tiếp có màu giống màu vân trung tâm, có 2 vị trí vân sáng bức xạ 1 trùng với bức xạ 2, 3 vị trí vân sáng bức xạ 1 trùng với bức xạ 3.
=> Số vân sáng quan sát được là N = (12 – 1)+ (9 – 1) + (8 – 1) – (2 + 3) = 21 vân
(2 vân sáng trùng nhau tính là 1)

Đáp án C
Ba vân trùng nhau nên ta có x1 = x2 = x3
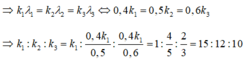
Vậy tại vị trí trùng nhau đầu tiên của 3 bức xạ tính từ vân trung tâm thì đó là vân sáng bậc 15 của λ1, vân sáng bậc 12 của λ2 và vân sáng bậc 10 của λ3.
Xét các vị trí trùng nhau của λ1 và λ2: 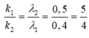
Vậy với các giá trị của k1 chia hết cho 5 thì là giá trị của k ứng với vị trí trùng nhau của λ1 và λ2 => có 2 vân trùng.
Xét các vị trí trùng nhau của λ1 và λ3: 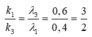
Vậy với các giá trị của k1 chia hết cho 3 thì là giá trị của k ứng với vị trí trùng nhau của λ1 và λ3 => có 4 vân trùng.
Xét các vị trí trùng nhau của λ3 và λ2: 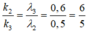
Vậy với các giá trị của k2 chia hết cho 6 thì là giá trị của k ứng với vị trí trùng nhau của λ3 và λ2 => có 1 vân trùng.
Vậy số vân sáng quan sát được trong khoảng giữa hai vân trùng nhau của 3 bức xạ là: 14 + 11 + 9 – 2 – 4 – 1 = 27 vân sáng.

Chọn B
Ta có i1 = 1,8 mm ứng với λ = 0,6μm.
i12 = 3,6 mm => λ12 = 1,2μm.
Ở đây λ12 chỉ chia hết cho λ = 0,4μm.

Bạn tham khảo một bài hoàn toàn tương tự như vậy nhé
Câu hỏi của trần thị phương thảo - Học và thi online với HOC24

@Tuấn: Bạn suy luận gần đúng rồi, nhưng chỉ có một chút sai sót ở đây,
Đó là, bạn tìm k = 9, thì do tính đối xứng qua vân trung tâm, nửa trên và dưới thỏa mãn 4,5.i2
--> Có 9 vân sáng của lambda 2
bài làm
do có 7 vân sáng suy ra có 6 khoảng vân
suy ra 6i1=ki2 suy ra 6 lamđa1= k lamđa2 suy ra k=9 (có 10 vân sáng)
khoảng cách gần nhất từ vân trung tâm đến vân sáng cùng màu vs nó là x= 2i1
suy ra chỉ có 3 điểm trùng vân sáng. số vân sáng trên đoạn đó là 10+7-3= 14 vân
nhưng đáp số lại ghi 13 vân. mong thầy giảng giúp em ạ.