Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo tính chất đường trung tuyến trong tam giác vuông thì ta có:
\(AG=2.GM=\frac{2}{3}AM=\frac{2}{3}.12=8\)(cm)
\(\Rightarrow GM=8:2=4\)(cm)

Vì G là trọng tâm của ABC nên
AG = 2/3AM
=> GM = AM - AG = AM - 2/3AM = 1/3AM
Vậy \(\frac{GM}{AM}=\frac{1}{3}\)

Xét tam giác ABC có AM là đường trung tuyến
=>AG= 2/3AM
AM=6:2/3
AM=9
=>GM=1/3AM
GM=1/3*9
GM=3
AM=

vì G là trọng tâm của tam giác ABC
AM là đường trung tuyến của tam giác ABC
=> AM = \(\dfrac{3}{2}AG\)
AM = \(\dfrac{3}{2}.9\)
AM = \(\dfrac{27}{2}=13,5\left(cm\right)\)
=>GM = \(\dfrac{1}{3}AM\)
GM = \(\dfrac{1}{3}.13,5\) = 4,5 (cm)

Vì G là trọng tâm tam giác ABC nên GM = 1/2 AG = 1/2.10 = 5cm. Chọn B

Vì `G` là trọng tâm của tam giác
`@` Theo tính chất của trọng tâm (cách đỉnh `2/3,` cách đáy `1/3`)
`-> GA = 2GM, GA= 2/3 AM`
Xét các đáp án trên `-> D.`

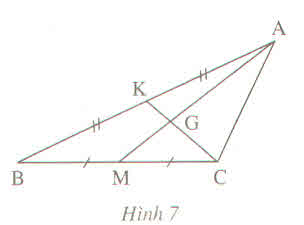
a) Vì G là trọng tâm của tam giác AEF với đường trung tuyến AM nên theo định lí 3 đường trung tuyến cắt nhau tại trọng tâm ta có :
\(\dfrac{{AG}}{{AM}} = \dfrac{2}{3}\)\( \Rightarrow \dfrac{{GM}}{{AM}} = 1 - \dfrac{2}{3} = \dfrac{1}{3}\)
b) Vì \(\dfrac{{AG}}{{AM}} = \dfrac{2}{3}\) và \(\dfrac{{GM}}{{AM}} = \dfrac{1}{3}\)(theo câu a)
\( \Rightarrow \dfrac{{GM}}{{AG}} = \dfrac{1}{2}\)
c) Vì \(\dfrac{{GM}}{{AG}} = \dfrac{1}{2}\)(chứng minh b)
\( \Rightarrow \dfrac{{AG}}{{GM}} = 2\)