Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Suy luận C là chính xác do \(0< x< 1\) nên x > 0 nên nhân hai vế của bất phương trình \(y< 1\) với x ta được \(xy< x\) và do x < 1 nên theo tính chất bắc cầu của bất phương trình ta được: \(xy< 1\).

Mệnh đề B và D đều sai
Mệnh đề B chỉ đúng khi a;b;c;d dương
Mệnh đề D thì sai rõ ràng

sử dụng phương pháp thế nha bn , rút 1 ẩn từ phương trình đơn giản rồi thế vào phương trình còn lại rồi giải bình thường . tập làm đi cho quen nha bn :)

a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
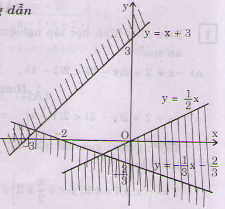
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
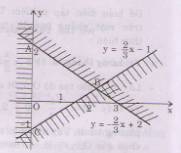

a) \(x^2\ge4x\)(1)
Nếu \(\left[{}\begin{matrix}x_1=0\\x_2=4\end{matrix}\right.\) \(\Rightarrow VT=VP\)
Nếu \(x< 0\Rightarrow VT>0;VP< 0\)=> \(VT>VP\)
Nếu 0<x<4 \(\Rightarrow VT< VP\)
nếu x> 4\(\Rightarrow VT>VP\)
Kết luận nghiệm BPT (1): \(\left[{}\begin{matrix}x\le0\\x\ge4\end{matrix}\right.\)
b)
(1) \(\Rightarrow\left[{}\begin{matrix}x< \dfrac{3-\sqrt{5}}{2}\\x>\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)
(2) \(\Rightarrow-2\le x\le3\)
KL nghiệm
\(\left[{}\begin{matrix}-2\le x< \dfrac{3-\sqrt{5}}{2}\\\dfrac{3+\sqrt{5}}{2}< x\le3\end{matrix}\right.\)
a)\(Bpt\Leftrightarrow\) \(\left\{{}\begin{matrix}x^2-4x\ge0\left(1\right)\\\left(2x-1\right)^2-9>0\left(2\right)\end{matrix}\right.\)
Giải (1): \(x^2-4x\ge0\Leftrightarrow\left[{}\begin{matrix}x\ge4\\x\le0\end{matrix}\right.\)
Giải (2): \(\left(2x-1\right)^2-9=\left(2x-1\right)^2-3^2=\left(2x-4\right)\left(2x+2\right)\)
\(\left(2x-4\right)\left(2x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Vì vậy: \(\left(2x-1\right)^2-9< 0\Leftrightarrow-1< x< 2\).
Kết hợp điều kiện \(\left(1\right)\) và \(\left(2\right)\) suy ra: \(-1< x\le0\) thỏa mãn hệ bất phương trình.

\(\left\{{}\begin{matrix}3x+2y=7\\x^2+y^2-7x+xy=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+2y=7\\x^2+y^2-3x^2-2xy+xy=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+2y=7\\-2x^2-xy+y^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+2y=7\\-\left(x+y\right)\left(2x-y\right)=0\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}3x+2y=7\\x+y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=-7\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}3x+2y=7\\2x-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy .......

1. \(\left\{{}\begin{matrix}x+y+\dfrac{1}{x}+\dfrac{1}{y}=5\\x^2+y^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}=9\end{matrix}\right.\) ĐKXĐ : \(\left\{{}\begin{matrix}x>0\\y>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2y+xy^2+x+y=5xy\\x^4y^2+x^2y^4+x^2+y^2=9x^2y^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^4y^2+x^2y^4+x^2+y^2=25x^2y^2\\x^4y^2+x^2y^4+x^2+y^2=9x^2y^2\end{matrix}\right.\)\(\Leftrightarrow0=16x^2y^2\)
\(\Rightarrow\) phương trình vô nghiệm


C.
Chọn C