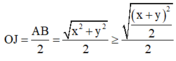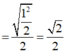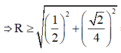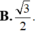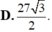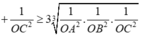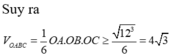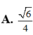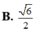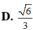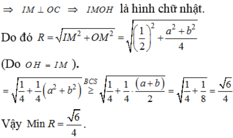Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\widehat{xOz}=80^0+20^0=100^0\)
b: \(\widehat{zOm}=\dfrac{\widehat{yOz}}{2}=10^0\)
\(\Leftrightarrow\widehat{xOm}=90^0\)

Bổ sung giả thiết là \(n\) điểm đó nằm trên \(xy\)
Số các tia có gốc O là \(n\).
Ta nhận thấy số các tia có gốc là các điểm \(A_i\left(1\le i\le n\right)\) chính là \(A^2_n=\dfrac{n!}{\left(n-2\right)!}=n\left(n-1\right)=n^2-n\)
Từ đề bài, ta suy ra \(n^2-n+n=40\Leftrightarrow n^2=40\), vô lí.
(Mình nghĩ đề bài là 49 tia thì khi đó \(n=7\))

Đáp án C
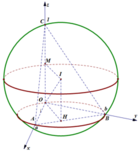
Phương pháp: Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp khối chóp.
Cách giải: Đặt A(x;0;0), B(0;y;0), (x,y>0)
Vì OA+OB=OC = 1 => x+y=1
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G
Tam giác OAB vuông tại O => J là tâm đường tròn ngoại tiếp tam giác
![]()
![]()
mà F là trung điểm của OC
=>GF là đường trung trực của OC => GC=GO
=> GO=GA=GB=GC=> G là tâm mặt cầu ngoại tiếp tứ diện OABC.
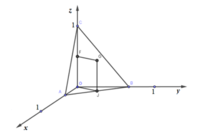
Bán kính mặt cầu ngoại tiếp tứ diện OABC
![]()
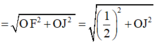
Ta có: