Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chiều cao của cột cờ là:
\(10.5\cdot tan\left(35^045'\right)\simeq7,56\left(m\right)\)

Bài 2
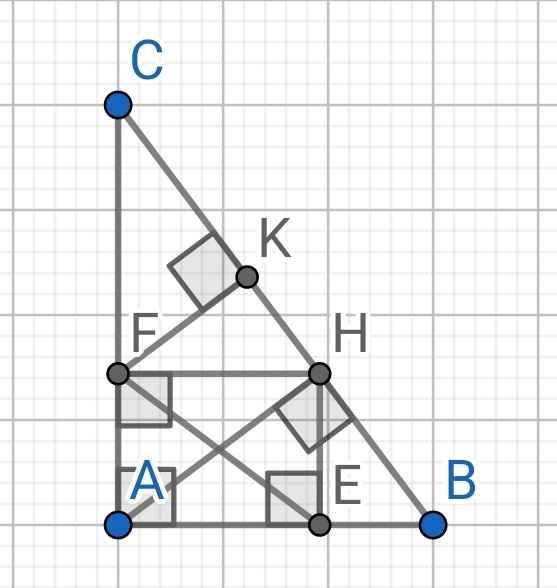 a) ∆ABC vuông tại A, AH là đường cao
a) ∆ABC vuông tại A, AH là đường cao
⇒ AH² = BH.HC
= 4.9
= 36
⇒ AH = 6 (cm)
BC = BH + HC
= 4 + 9 = 13 (cm)
∆ABC vuông tại A, AH là đường cao
⇒ AB² = BH.BC
= 4.13
= 52 (cm)
⇒ AB = 2√13 (cm)
⇒ cos ABC = AB/BC
= 2√13/13
⇒ ∠ABC ≈ 56⁰
b) ∆AHB vuông tại H, HE là đường cao
⇒ AH² = AE.AB (1)
∆AHC vuông tại H, HF là đường cao
⇒ AH² = AF.AC (2)
Từ (1) và (2) suy ra:
AE.AB + AF.AC = 2AH² (3)
Xét tứ giác AEHF có:
∠HFA = ∠FAE = ∠AEH = 90⁰ (gt)
⇒ AEHF là hình chữ nhật
⇒ AH = EF (4)
Từ (3) và (4) suy ra:
AE.AB + AF.AC = 2EF²
Bài 1
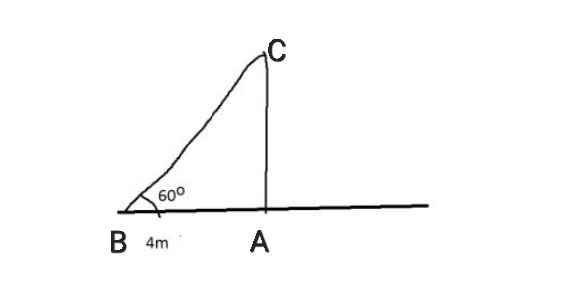 Ta có:
Ta có:
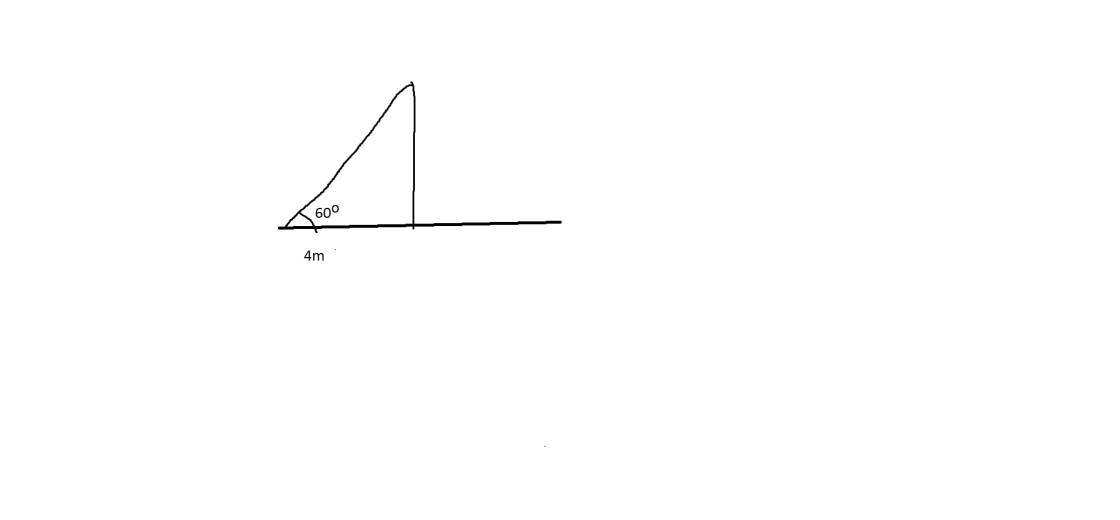
tan B = AC/AB
⇒ AC = AB . tan B
= 4 . tan60⁰
= 4√3 (m)
≈ 7 (m)

Chiều cao của cái cây đó là:
4,5*tan55\(\simeq6,43\left(m\right)\)

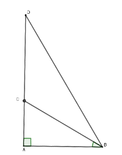
Từ giả thiết ra có chiều dài ban đầu của cây là AD; sau khi bị sét đánh thì cây còn lại AC = 1; C B A ^ = 40 0 và CD = CB
Xét tam giác ∆ ABC vuông tại A có BC = A C sin 40 o = 1,56m nên CD = 1,56m
Suy ra AD = AC + CD = 1 + 1,56 = 2,56m
Đáp án cần chọn là: D

60 A B C 8m
\(\tan\widehat{BCA}=\dfrac{AB}{AC}=\dfrac{AB}{8}\Rightarrow\tan60^o=\dfrac{AB}{8}\Rightarrow AB=8\sqrt{3}\left(cm\right)\)

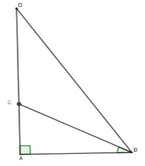
Từ giả thiết ra có chiều dài ban đầu của cây là AD; sau khi bị sét đánh thì cây còn lại AC = 1,5; C B A ^ = 35 0 và CD = CB
Xét tam giác ABC vuông tại A có BC = A C sin 35 o ≈ 2,6m
Suy ra AD = AC + CD = 1,5 + 2,6 = 4,1m
Vậy cây cao 4,1m
Đáp án cần chọn là: C
Vật lý 8
Gọi chân cây là A, đỉnh cây là B , điểm dài nhất bóng cây là C
Ta có góc BCA =60 độ
nên góc ABC =30 độ
Đối diện với cạnh góc vuông là 1 góc nhọn 30 độ thì cạnh góc vuông đó = 1/2 cạnh huyền
Do đó BC=2AC=2.4=8 (m)
Tam giác ABC vuông tại A áp dụng định lý Pytago ta có
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2=BC^2-AC^2=8^2-4^2\)
\(\Rightarrow AB^2=48\)
\(\Rightarrow AB=\sqrt{48}\)(m)
Vậy chiều cao cây dừa là căn 48m