Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3. Gọi d là ƯCLN(2n + 3, 4n + 8), d ∈ N*
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\4n+8⋮d\end{cases}\Rightarrow}\hept{\begin{cases}4n+6⋮d\\4n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\in\left\{1;2\right\}\)
Mà 2n + 3 không chia hết cho 2
\(\Rightarrow d=1\)
\(\RightarrowƯCLN\left(2n+3,4n+8\right)=1\)
\(\Rightarrow\frac{2n+3}{4n+8}\) là phân số tối giản.

(làm câu dễ nhất...> . < ...)
c)Để \(\dfrac{6}{n-1}\) là số nguyên thì 6 ⋮ \(n-1\)
\(\Rightarrow n-1\inƯ\left(6\right)=\left\{\pm1,\pm2,\pm3,\pm6\right\}\)
Ta có bảng sau :
n-1 n -1 -2 -3 -6 1 2 3 6 0 -1 -2 -5 2 3 4 7
Vậy để \(\dfrac{6}{n-1}\) là số nguyên thì \(x=\left\{0;-1;-2;-5;2;3;4;7\right\}\)
d) \(\dfrac{n}{n-2}=\dfrac{n-2+2}{n-2}\) là số nguyên thì \(n-2+2⋮n-2\Rightarrow2⋮n-2\Rightarrow n-2\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Ta có bảng sau:
n-2 n -1 -2 1 2 1 3 0 4 Vậy với \(x=\left\{1;3;0;4\right\}\) thì \(\dfrac{n}{n-2}\) là số nguyên
(chắc sai... > . < ...)

BÀi 1
Để A \(\in\) Z
=>\(\left(n+2\right)⋮\left(n-5\right)\)
=>\([\left(n-5\right)+7]⋮\left(n-5\right)\)
=>\(7⋮\left(n-5\right)\)
=>\(n-5\in\left\{1;7;-1;-7\right\}\)
=>\(n\in\left\{6;13;4;-2\right\}\)
Vậy \(n\in\left\{6;13;4;-2\right\}\)

Bài 1 :
Sửa đề :
Tìm \(n\in Z\) để những phân số sau đồng thời có giá trị nguyên
\(\dfrac{-12n}{n};\dfrac{15}{n-2};\dfrac{8}{n+1}\)
Làm
Ta có :
\(\dfrac{-12n}{n}=-12\)
\(\Leftrightarrow\) Với mọi \(n\) thì \(\dfrac{-12n}{n}\) đều có giá trị nguyên \(\left(1\right)\)
Để \(\dfrac{15}{n-2}\in Z\) \(\Leftrightarrow n-2\inƯ\left(15\right)=\left\{\pm1;\pm15;\pm3;\pm5\right\}\)
\(\Leftrightarrow n\in\left\{-13;\pm3;\pm1;5;7;17\right\}\left(1\right)\)
Để \(\dfrac{8}{n+1}\in Z\Leftrightarrow n+1\inƯ\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
\(\Leftrightarrow n\in\left\{-9;-5;\pm3;-2;0;1;7\right\}\left(3\right)\)
Từ \(\left(1\right)+\left(2\right)+\left(3\right)\Leftrightarrow n\in\left\{\pm3;1;7\right\}\)

Bài 1:
a) \(\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
Quy đồng \(VP\) ta được:
\(VP=\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(\Rightarrow VP=\dfrac{n+1}{n\left(n+1\right)}-\dfrac{n}{n\left(n+1\right)}\)
\(\Rightarrow VP=\dfrac{n+1-n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}\)
\(\Rightarrow VP=VT\)
Vậy \(\forall n\in Z,n>0\Rightarrow\dfrac{1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\) (Đpcm)
b) \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(=1-\dfrac{1}{10}\)
\(=\dfrac{9}{10}\)
Bài 3:
a) \(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{1+1}{n\left(n+1\right)}-\dfrac{n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}\)
b) A=\(\dfrac{1}{2}.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{4}+\dfrac{1}{4}.\dfrac{1}{5}+\dfrac{1}{5}.\dfrac{1}{6}+\dfrac{1}{6}.\dfrac{1}{7}+\dfrac{1}{7}.\dfrac{1}{8}+\dfrac{1}{8}.\dfrac{1}{9}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}\)
\(=\dfrac{1}{2}-\dfrac{1}{9}\)
\(=\dfrac{7}{18}\)
B=\(\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}+\dfrac{1}{132}\)
\(=\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}+\dfrac{1}{10.11}+\dfrac{1}{11.12}\)
\(=\dfrac{1}{5}-\dfrac{1}{12}\)
\(=\dfrac{7}{60}\)
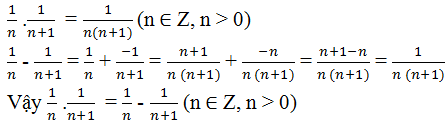

a) \(\dfrac{n+2}{3}\) là số tự nhiên khi
\(n+2⋮3\)
\(\Rightarrow n+2\in\left\{1;3\right\}\)
\(\Rightarrow n\in\left\{-1;1\right\}\left(n\in Z\right)\)
b) \(\dfrac{7}{n-1}\) là số tự nhiên khi
\(7⋮n-1\)
\(\Rightarrow7n-7\left(n-1\right)⋮n-1\)
\(\Rightarrow7n-7n+7⋮n-1\)
\(\Rightarrow7⋮n-1\)
\(\Rightarrow n-1\in\left\{1;7\right\}\Rightarrow\Rightarrow n\in\left\{2;8\right\}\left(n\in Z\right)\)
c) \(\dfrac{n+1}{n-1}\) là sô tự nhiên khi
\(n+1⋮n-1\)
\(\Rightarrow n+1-\left(n-1\right)⋮n-1\)
\(\Rightarrow n+1-n+1⋮n-1\)
\(\Rightarrow2⋮n-1\)
\(\Rightarrow n-1\in\left\{1;2\right\}\Rightarrow n\in\left\{2;3\right\}\left(n\in Z\right)\)