Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách suy luận của em như vậy là đúng rồi.
Nếu cảm ứng từ tạo với pháp tuyến khung dây 1 góc 300 thì ta lấy \(\varphi = \pm\dfrac{\pi}{6}\)
Thông thường, các bài toán dạng này thì người ta sẽ hỏi theo hướng ngược lại, là biết \(\varphi\) rồi tìm góc tạo bởi giữa véc tơ \(\vec{B}\) với véc tơ pháp tuyến \(\vec{n}\), như thế chỉ có 1 đáp án duy nhất.

Thưa thầy ,
Em có ý kiến như thế này " Em thấy ở trên Online Math mới có phần gọi là tuyển CTV , em rất muốn tham gia chức vụ ở trên trang web Học 24 " . Vì vậy em muốn ở web Học 24 này cũng có đợt tuyển CTV và em sẽ tham gia ạ . Mong là Học 24 sẽ đồng ý với yêu cầu này !

Công thức của em hoàn toàn đúng rồi.
Đối với 2 đoạn mạch vuông pha (uRL và um) thì em chỉ cần sử dụng điều kiện vuông pha của 2 đoạn mạch này là: \(\tan\varphi_{RL}.\tan\varphi_m=-1\)
Đề bài này có vấn đề vì để uRL vuông pha với um thì ZC > ZL, nhưng đề bài lại cho ZC < ZL

Lý luận của em đúng rồi, cộng hưởng không ảnh hưởng gì cả.
Mình hướng dẫn lại thế này nhé.
\(U_C=IZ_C=\frac{U}{\sqrt{R^2+\left(Z_L-Z_C\right)^2}}.Z_C\)
\(=\frac{U}{\sqrt{L^2\omega^4+\left(R^2-\frac{2L}{C}\right)\omega^2+\frac{1}{C^2}}}\)
Đặt \(X=L^2\omega^4+\left(R^2-\frac{2L}{C}\right)\omega^2+\frac{1}{C^2}\)
\(\Rightarrow X=\frac{\omega^4}{10}-10^4.\omega^2+10^9\)
Khi đó, Uc max thì X min và ngược lại
Đặt \(t=\omega^2\), \(2,5.10^4\le t\le10.10^4\)
\(\Rightarrow X=\frac{t^2}{10}-10^4t+10^9\)
\(X'=\frac{t}{5}-10^4=0\Rightarrow t=5.10^4\)
Từ đó suy ra Uc max khi \(t=5.10^4\), và min khi \(t=10.10^4\)
Từ đó suy ra giá trị min, max của Uc
@phynit: thầy ơi bài giải đáp án thì đúng rồi nhưng cách suy ngĩ trên của em là mâu thuẫn phải không thầy
nhìn thì rõ ràng t=5*10^4 của thầy xấp xỉ 71pi
và t=10*10^4 xấp xỉ 100pi
mà w max của em ngoài khoảng trên là 115pi. 100pi gần hơn 71pi mà 71pi lại là Umax
có lẽ dạng parabol đó chỉ áp dụng cho R, L hoặc C biến thiên thôi phải không thầy.

Để tăng hiệu suất của máy biến áp thì giảm công suất tỏa nhiệt trên máy biến áp.
A. Giảm R --> Giảm công suất --> OK
B. Dùng lõi sắt có điện trở suất nhỏ ko đc vì lõi sắt này không dẫn điện, nên điện trở suất không ảnh hưởng. Phải thay là lõi sắt dẫn từ tốt.
C. Dùng lõi sắt gồm nhiều lá thép mỏng ghép cách điện --> Triệt tiêu dòng điện Fuco --> Giảm công suất.
D. Đặt lá sắt song song với mặt phẳng chứa đường sức từ để đường sức này chỉ nằm trong lõi sắt --> từ trường truyền đi tốt nhất.

A. Đúng, vì \(i_m=i_R+i_L+i_C\)
B. Đúng, vì \(u_m=u_R+u_L+u_C\)
C. Đúng, vì: \(P=I^2.\Sigma R=\Sigma\left(I^2R\right)\)
D. Sai, vì khi mắc thêm thì P có thể tăng hoặc giảm

Uh, theo suy luận của bạn mình thấy cũng có lý :)
Tuy nhiên, bài toán này mình thấy nó khá mập mờ, chẳng có phương án nào hợp lý cả.
Bài này đúng là cần dùng phương pháp loại trừ, tuy nhiên ở đây mình loại trừ D, vì nếu tia ló // với AC thì sẽ chẳng có tia nào ló ra cả vì thằng đỏ trung với cạnh AC thì các tia màu khác sẽ bị phản xạ toàn phần.
Đáp án C là hợp lý.

Đáp án sai là C, vì khi tăng hệ số công suất ==> Dòng điện tiêu thụ giảm ==> Giảm hao phí ==> Có lợi.

Đáp án D
+ Giá trị trung bình của phép đo
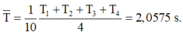
![]()
Nếu lấy hai chữ số có nghĩa ở sai số tuyệt đối thì kết quả phép đo là
![]()
Điện xoay chiều thú vị ở chỗ đó, chúng ta có thể dùng biến đổi đại số, dùng giản đồ véc tơ (tạm gọi là véc tơ thường - véc tơ buộc và véc tơ trượt), ngoài ra còn có thể dùng số phức để giải. Tùy từng bài toán và tùy từng kinh nghiệm của mỗi người thì sẽ biết nên làm theo cách nào cho hợp lí. Em hãy cứ làm nhiều bài tập điện xoay chiều thì em sẽ nhận ra điều đó.
Dùng giản đồ véc tơ thường thì hầu như dạng bài tập nào cũng giải được.
Còn véc tơ trượt là một biến thể của véc tơ thường (dựa vào tính chất cộng véc tơ trong toán học), làm cho hình vẽ đỡ rối hơn.
Còn nên dùng theo cách nào thì như mình nói tùy từng bài toán và kinh nghiệm của mỗi người. Kinh nghiệm của mình là những bài toán mà cho mối liên hệ các điện áp chéo nhau (VD: URL, URC,...) thì dùng véc tơ thường, trường hợp còn lại thì dùng véc tơ trượt.
vâng em cảm ơn thầy ạ.