
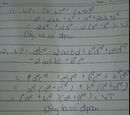
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

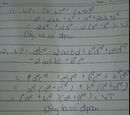

\(\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\frac{a+b+c}{abc}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\left(a+b+c=0\right)\)
=> điều phải cm

a.
\(\frac{x^2}{4}+x+3=\frac{x^2}{4}+x+1+2=\left(\frac{x}{2}+1\right)^2+2>0;\forall x\)
b.
\(A=-3x^2+2x-5=-3\left(x^2-2.\frac{1}{3}x+\frac{1}{9}\right)-\frac{14}{3}=-3\left(x-\frac{1}{3}\right)^2-\frac{14}{3}\le-\frac{14}{3}\)
\(A_{max}=-\frac{14}{3}\) khi \(x=\frac{1}{3}\)
c.
Đề thiếu (để ý 2 số hạng cuối)
\(A=x^4-2x^3+x^2+3x^2-6x+3-1\)
\(=\left(x^2-x\right)^2+3\left(x-1\right)^2-1\ge-1\)
\(A_{min}=-1\) khi \(x=1\)
d.
\(27x^2-\frac{9}{2}x+\frac{3}{16}=3\left(9x^2-\frac{3}{2}x+\frac{1}{16}\right)=3\left(3x-\frac{1}{4}\right)^2\)
e.
\(=\left[\left(b+c\right)+a\right]^2+\left[\left(b+c\right)-a\right]^2+\left[a-\left(b-c\right)\right]^2+\left[a+\left(b-c\right)\right]^2\)
\(=2\left(b+c\right)^2+2a^2+2a^2+2\left(b-c\right)^2\)
\(=4a^2+2b^2+4bc+2c^2+2b^2-4bc+2c^2\)
\(=4\left(a^2+b^2+c^2\right)\)
f.
\(\left(a^2+b^2\right)\left(c^2+d^2\right)=a^2c^2+b^2d^2+a^2d^2+b^2c^2\)
\(=\left(a^2c^2+b^2d^2+2ac.bd\right)+\left(a^2d^2+b^2c^2-2ad.bc\right)\)
\(=\left(ac+bd\right)^2+\left(ad-bc\right)^2\)

\(\left(A+B\right)^2=A^2+2AB+B^2\)
\(\left(A+B\right)^3=A^3+3A^2B+3AB^2+B^3\)
\(A^2-B^2=\left(A-B\right)\left(A+B\right)\)
2
a
\(15x^2y^3z^2-20x^2yz^2+10xy^3z\)
\(=5xyz\left(3xy^2z-4xz+2y^2\right)⋮5xyz\)
b
\(13ab^2+abc+32a=a\left(13b^2+bc+32\right)\)
TH1:\(13b^2+bc+32=7b\cdot P\left(x\right)\) thì A chia hết cho B
TH2:\(13b^2+bc+32=7b\cdot Q\left(x\right)+r\left(r>0\right)\) thì A không chia hết cho B

Bài 2:
a: \(A=1999\cdot2001\)
\(=\left(2000-1\right)\left(2000+1\right)\)
\(=2000^2-1< 2000^2=B\)
Do đó: B lớn hơn
b: \(C=\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\)
\(=\left(2-1\right)\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\)
\(=2^{16}-1< 2^{16}=D\)
Do đó: D lớn hơn

a) Ta có: \(4b^2c^2-\left(b^2+c^2-a^2\right)^2\)
\(=\left(2bc-b^2-c^2+a^2\right)\left(2bc+b^2+c^2-a^2\right)\)
\(=-\left(b^2-2bc+c^2-a^2\right)\left[\left(b^2+2bc+c^2\right)-a^2\right]\)
\(=-\left[\left(b^2-2bc+c^2\right)-a^2\right]\left[\left(b+c\right)^2-a^2\right]\)
\(=-\left[\left(b-c\right)^2-a^2\right]\left(b+c-a\right)\left(b+c+a\right)\)
\(=-\left(b-c-a\right)\left(b-c+a\right)\left(b+c-a\right)\left(b+c+a\right)\)



\(P=\left(x-y\right)^2+\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)-4x^2=\left(x-y-x-y\right)^2-\left(2x\right)^2=\left(-2y\right)^2-\left(2x\right)^2\)
\(=\left(2y-2x\right)\left(2y+2x\right)=2\left(y-x\right)2\left(y+x\right)=4\left(x+y\right)\left(y-x\right)\)
\(x^3-x^2y+3x-3y=x^2\left(x-y\right)+3\left(x-y\right)=\left(x-y\right)\left(x^2+3\right)\)
\(x^3-2x^2-4xy^2+x=x\left(x^2-2x+1-4y^2\right)=x\left[\left(x-1\right)^2-\left(2y\right)^2\right]=x\left(x+2y-1\right)\left(x-2y-1\right)\)
\(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-8=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-8\)
Đặt \(x^2+7x+10=t\), ta có:
\(t\left(t+2\right)-8=t^2+2t-8=t^2-2t+4t-8=t\left(t-2\right)+4\left(t-2\right)=\left(t-2\right)\left(t+4\right)\)
\(=\left(x^2+7x+10+4\right)\left(x^2+7x+10-2\right)=\left(x^2+7x+14\right)\left(x^2+7x-8\right)\)

2)
Xét hiệu:
\(A^2+B^2+C^2+D^2+4-2A-2B-2C-2D\)
\(=\left(A^2-2A+1\right)+\left(B^2-2B+1\right)+\left(C^2-2C+1\right)+\left(D^2-2D+1\right)\)
\(=\left(A-1\right)^2+\left(B-1\right)^2+\left(C-1\right)^2+\left(D-1\right)^2\ge0\)
=> BĐT luôn đúng
Vậy \(A^2+B^2+C^2+D^2+4\ge2\left(A+B+C+D\right)\)
1)
Áp dụng BĐT Cauchy cho 2 số không âm, ta có:
\(\dfrac{AB}{C}+\dfrac{BC}{A}\ge2\sqrt{\dfrac{AB}{C}.\dfrac{BC}{A}}=2B\) (1)
\(\dfrac{BC}{A}+\dfrac{AC}{B}\ge2\sqrt{\dfrac{BC}{A}.\dfrac{AC}{B}}=2C\) (2)
\(\dfrac{AB}{C}+\dfrac{AC}{B}\ge2\sqrt{\dfrac{AB}{C}.\dfrac{AC}{B}}=2A\) (3)
Từ (1)(2)(3) cộng vế theo vế:
\(2\left(\dfrac{AB}{C}+\dfrac{AC}{B}+\dfrac{BC}{A}\right)\ge2\left(A+B+C\right)\)
\(\Rightarrow\dfrac{AB}{C}+\dfrac{AC}{B}+\dfrac{BC}{A}\ge A+B+C\)

3a2c2 + bd + 3abc + acd
= 3ac(ac + b) + d(ac + b)
= (ac + b)(3ac + d)
ab(a + b) - bc(a + c) + abc
= b(a2 + ab - ac - c2 + ac)
= b(a2 + ab - c2)
a(b2 + c2) + b(c2 + a2) + c(a2 + b2) + 2abc
= ab2 + ac2 + bc2 + a2b + c(a2 + 2ab + b2)
= c2(a + b) + ab(a + b) + c(a + b)2
= (a + b)(c2 + ab + ac + bc)
= (a + b)[c(b + c) + a(b + c)]
= (a + b)(a + c)(b + c)
bc(b + c) + ac(c - a) - ab(a + b)
= bc(b + c) + ac[(b + c) - (a + b)] - ab(a + b)
= bc(b + c) + ac(b + c) - ac(a + b) - ab(a + b)
= c(b + c)(a + b) - a(a + b)(b + c)
= (a + b)(b + c)(c - a)