Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc ban đầu của người đó là x(km/h)
(ĐIều kiện: x>0)
Thời gian dự kiến của người đó sẽ đi hết quãng đường là \(\dfrac{36}{x}\left(h\right)\)
Độ dài nửa quãng đường còn lại là: 36*1/2=18(km)
Thời gian đi nửa quãng đường đầu tiên là \(\dfrac{18}{x}\left(giờ\right)\)
vận tốc của người đó ở 18km còn lại là x+2(km/h)
Thời gian người đó đi hết 18km còn lại là \(\dfrac{18}{x+2}\left(h\right)\)
Theo đề, ta có phương trình:
\(\dfrac{18}{x}+\dfrac{18}{x+2}+\dfrac{3}{10}=\dfrac{36}{x}\)
=>\(\dfrac{18}{x+2}-\dfrac{18}{x}=-\dfrac{3}{10}\)
=>\(\dfrac{6}{x}-\dfrac{6}{x+2}=\dfrac{1}{10}\)
=>\(\dfrac{6x+12-6x}{x\left(x+2\right)}=\dfrac{1}{10}\)
=>\(\dfrac{12}{x\left(x+2\right)}=\dfrac{1}{10}\)
=>x(x+2)=120
=>\(x^2+2x-120=0\)
=>\(\left(x+12\right)\left(x-10\right)=0\)
=>\(\left[{}\begin{matrix}x+12=0\\x-10=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-12\left(loại\right)\\x=10\left(nhận\right)\end{matrix}\right.\)
Vậy: Vận tốc ban đầu là 10km/h
Thời gian xe lăn bánh trên đường là \(\dfrac{36}{10}=3,6\left(giờ\right)\)

Gọi vận tốc ban đầu của người đó là a(km/h) \((a>0)\)
Theo đề,ta có: \(\dfrac{48}{a}+\dfrac{2}{13}+\dfrac{48}{a+2}=\dfrac{96}{a}\)
\(\Leftrightarrow\dfrac{48}{a}=\dfrac{2a+628}{13\left(a+2\right)}\Leftrightarrow624a+1248=2a^2+628a\)
\(\Leftrightarrow2a^2+4a-1248=0\Rightarrow a^2+2a-624=0\)
\(\Leftrightarrow\left(a+26\right)\left(a-24\right)=0\) mà \((a>0)\Rightarrow a=24\)
\(\Rightarrow\) thời gian lăn bánh là \(\dfrac{96}{24}-\dfrac{2}{13}=\dfrac{50}{13}\left(h\right)\)

Gọi vận tốc dự định đi của người đó là x (km/h) (x > 0)
Thời gian dự định đi của người đó là 36/x (h)
Thời gian người đó đi nửa quãng đường đầu là 18/x (h)
Nửa quãng đường sau người đó đi với vận tốc là x + 2 (km/h) và thời gian người đó đi là 18/(x+2) (h)
Vì nghỉ lại 30 phút nên thời gian đi từ lúc xuất phát đến khi tới B là 18 x + 1 2 + 18 x + 2
Do người đó đến B chậm hơn dự kiến 12 phút = 1/5h nên ta có phương trình:
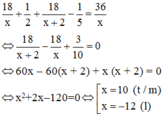
Vậy vận tốc của người đi xe đạp trên đoạn đường cuối của đoạn AB là 12 km/h
Đáp án: A

Gọi vận tốc của người đi xe đạp lúc đầu là x(x>0)
Thời gian dự định đi hết quãng đường AB là : \(\frac{30}{x}\left(h\right)\)
Thời gian người đó đi hết nửa quãng đường đầu là : \(\frac{15}{x}\left(h\right)\)
Thời gian người đó đi hết nửa quãng đường sau là : \(\frac{15}{x+2}\left(h\right)\)
15 phút=\(\frac{1}{4}\)h Ta có:
\(\frac{30}{x}=\frac{15}{x}+\frac{1}{4}+\frac{15}{x+2}\)
\(\Leftrightarrow\frac{15}{x}-\frac{15}{x+2}=\frac{1}{4}\)
\(\Leftrightarrow\frac{1}{x}-\frac{1}{x+2}=\frac{1}{60}\)
\(\Leftrightarrow\frac{2}{x\left(x+2\right)}=\frac{1}{60}\)
\(\Leftrightarrow x\left(x+2\right)=120\)
\(\Leftrightarrow\orbr{\begin{cases}x=-12\\x=10\end{cases}\Rightarrow x=10}\)

Gọi vận tốc dự định là x
Vận tốc đi trên S còn lại là : x+10 Dk :x>0
Vì người đó đến B sớm hơn dự định 24phut (=0,4h) nên ta có pt :
40/x +80/x+10 +0,4 = 120/x
0,4 = 80/x - 80/x+10
0,4=800/x(x+10)
x2+10x=2000
x2+10x-2000=0
(x-40)(x+50)=0
Vi x>0 => x+50>0
=> x-40 =0
x=40(km/h)

Quãng đường AB dài là:
60 x 2 = 120 (km)
Nếu người đó đi với vận tốc 40km/h thì cần thời gian là:
120: 40 = 3 giờ