Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Xét tỉ số: \(\frac{x_M}{i}=3\)
\(\Rightarrow\) Tại M là vân sáng bậc 3.
Trong thí nghiệm Iâng về giao thoa ánh sáng, hai khe hẹp cách nhau một khoảng 0,5 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,5 m. Hai khe được chiếu bằng bức xạ có bước sóng 0,6 μmμm. Trên màn thu được hình ảnh giao thoa. Tại điểm M trên màn cách vân sáng trung tâm một khoảng 5,4 mm có
A. vân sáng bậc 2
B. vân sáng bậc 4
C. vân sáng bậc 3
D. vân sáng thứ 4

Đáp án C
D = 2 m, x = 6 mm, k = 5
Thay đổi khoảng cách hai khe hẹp một đoạn bằng 0,2 mm thì tại M có vân sáng bậc 6. Do x không thay đổi, mà 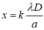
Suy ra k tỉ lệ thuận với a, như vậy khi chuyển từ vân sáng bậc 5 thành vân sáng bậc 6 thì a tăng => a’ = a + 0,2.10-3 (m).
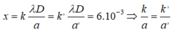
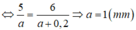
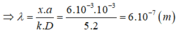

a. Bề rộng của 16 vân sáng là 15i, suy ra 15i=18mm --> i = 1,2 mm
Khoảng cách từ hai khe đến màn: \(D=\dfrac{ai}{\lambda}=\dfrac{1,2.1,2}{0,6}=2,4m\)
b. Bề rộng 21 vân sáng là 20 i', suy ra 20i' = 18mm ---> i'=0,9mm
Bước sóng: \(\lambda'=\dfrac{ai}{D}=\frac{1,2.0,9}{2,4}=0,45\mu m\)
c. Tại vị trí cách vân trung tâm x = 6mm
\(\Rightarrow x=6i=6,67i'\)
Nên tại vị trí này là vân sáng bậc 6 của bước sóng \(\lambda\)

Chú ý nên giữ nguyên đơn vị của a(mm); D(m); \(\lambda (\mu m)\)
Ví trí vân sáng đỏ bậc 2 và vân sáng tím bậc 2 lần lượt là
\(x_{sđỏ} = 2.i_{đỏ}= 2.\frac{\lambda_{đỏ}D}{a}.\)
\(x_{stím} = 2.i_{tím}= 2.\frac{\lambda_{tím}D}{a}.\)
=> \(x_{sđỏ}-x_{s tím}= 2.\frac{D}{a}(\lambda_{đỏ}-\lambda_{tím})=4,8mm.\)

Tại điểm M là vân sáng nên \(x_M=ki=k\frac{\lambda D}{a}\)
\(\lambda=\frac{x_Ma}{kD}=\frac{4,2.0,5}{k.1,4}=\frac{1,5}{k}\)
Theo giả thiết: \(0,38\le\lambda\le0,76\)
\(\Rightarrow0,38\le\frac{1,5}{k}\le0,76\)
\(\Rightarrow1,97\le k\le3,94\)
k nguyên nên k = 2,3.
Như vậy, tại M có 2 bước sóng cho vân sáng, đáp án là A.

Tóm tắt:
a = \(10^{-3}m\)
D = \(1,25m\)
\(\lambda_1=0,64\mu m\)
\(\lambda_2=0,48\mu m\)
\(\Delta x=?\)
Giải:
Khi vân sáng trùng nhau:
\(k_1\lambda_1=k_2\lambda_2\Rightarrow\)\(\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,48}{0,64}=\frac{3}{4}\)
Vậy: \(k_1=3;k_2=4\)\(\Rightarrow\Delta x=3i_1=3.\frac{\lambda_1.D}{a}=3.\)\(\frac{0,64.10^{-6}.1,25}{10^{-3}}=2,4.10^{-3}m=2,4mm\)
\(\rightarrow D\)

\(i = \frac{\lambda D}{a}=\frac{0,5.2}{0,5}= 2mm.\)
Số vân sáng trên màn quan sát là
\(N_s= 2.[\frac{L}{2i}]+1 =2.6+1 = 13.\)

Vân sáng bậc 4 cách vân trung tâm là
\(x_ 4 = 4.i = 4.\frac{\lambda D}{a} = 3,2mm.\)
Chú ý nếu giữ nguyênđơn vị của \(\lambda (\mu m)\), D(m), a(mm) thì khi đó kết quả cho \(x\) ra đơn vị là mm.

Tại vị trí cách vân trung tâm 3 mm có vân sáng bậc \(k\) của bức xạ \(\lambda\) khi
\(x=3mm = ki =k\frac{\lambda D}{a}.\)
=> \(\lambda = \frac{3.a}{D k}.(1)\)
Mặt khác : \(0,38 \mu m \leq \lambda \leq 0,76 \mu m.\)
<=> \(0,38 \mu m \leq \frac{3a}{kD} \leq 0,76 \mu m.\)
<=> \(\frac{3.0,8}{0,76.2} \leq k \leq \frac{3.0,8}{0,38.2} \)
Giữ nguyên đơn vị của \(x = 3mm; a = 0,8mm;\lambda = 0,76 \mu m;0,38 \mu m; D= 2m\)
<=> \(1,57 \leq k \leq 3,15.\)
<=> \(k = 2,3.\)
Thay vào (1) ta thu được hai bước sóng là \(\lambda_1 = \frac{3.0,8}{2.2}=0,6\mu m.\)
\(\lambda_2 = \frac{3.0,8}{3.2}=0,4\mu m.\)
Đáp án A
+ Theo giả thuyết bài toán, ta có