Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kính lúp đóng vai trò chính là màn hứng.
Lúc đầu: \(i = \frac{\lambda D}{a}= \frac{2,4}{16}= 0,15mm.(1)\)
\(i' = \frac{\lambda (D+0,3)}{a}= 0,24mm.\)
=> \(\frac{i}{i'}= \frac{D}{D+0,3}= \frac{5}{8}.\)
=> \(D = 0,5m.\)
Bước sóng của bức xạ là \(\lambda = \frac{ai}{D} = \frac{1,8.0,15}{0,5}=0,54 \mu m.\)

Gọi L là khoảng cách giữa hai vân sáng ngoài cùng
N là số vân sang quan sát được
Ta có hai trường hợp :
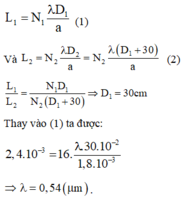
Đáp án B

Gọi D là khoảng cách từ màn mang hai khe F 1 , F 2 đến mặt phẳng tiêu vật của kính lúp, ở vị trí thứ nhất, và D + 30 là khoảng cách ở vị trí thứ hai. Ta có hai phương trình :
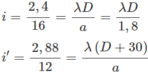
Giải ra ta được : D = 50 cm và λ = 0,54 μm.

Tịnh tiến màn quan sát lại gần mặt phẳng chưa hai khe 25 cm tức là \(D' = D-0,25.\)
\(i_1 = \frac{\lambda D}{a}\\
i_2 =\frac{\lambda (D-0,25)}{a} \)=> \(\frac{i}{i'}= \frac{D}{D-0,25}= \frac{5}{4}\)
=> \(D = 5.0,25 = 1,25m.\)
=> \(\lambda = \frac{i.a}{D}= 0,48 \mu m.\)
Chú ý là giữ nguyên đơn vị i (mm); a (mm) ; D (m) thì đơn vị bước sóng \(\lambda (\mu m)\).

Khi quan sát vân bằng kính lúp thì ta trông thấy ảnh của hệ vân nằm trên mặt phẳng tiêu vật của kính lúp và ảnh đó ở xa vô cùng (H.25.1G).
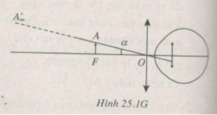
Ta thấy α = tan α = i/f = 12,5'
Khoảng cách từ hai khe tới mặt phẳng của các vân : D = L - f = 40 - 4 = 36 cm = 0,36 m.
Bước sóng của bức xạ là :
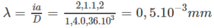

+ Xét tỉ số: \(\frac{x_M}{i}=3\)
\(\Rightarrow\) Tại M là vân sáng bậc 3.
Trong thí nghiệm Iâng về giao thoa ánh sáng, hai khe hẹp cách nhau một khoảng 0,5 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,5 m. Hai khe được chiếu bằng bức xạ có bước sóng 0,6 μmμm. Trên màn thu được hình ảnh giao thoa. Tại điểm M trên màn cách vân sáng trung tâm một khoảng 5,4 mm có
A. vân sáng bậc 2
B. vân sáng bậc 4
C. vân sáng bậc 3
D. vân sáng thứ 4

+ Ban đầu M là vân tối thứ 3 nên: \(x_M=\left(2+\frac{1}{2}\right)\frac{\lambda D}{a}\left(1\right)\)
+ Khi giãm S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc n nên: \(x_M=n\frac{\lambda D}{a-\Delta a}\left(2\right)\)
+ Khi tăng S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc 3n nên: \(x_M=3n\frac{\lambda D}{a+\Delta a}\left(3\right)\)
+ (2) và (3) \(\Rightarrow k\frac{\lambda D}{a-\Delta a}=3k\frac{\lambda d}{a+\Delta a}\Rightarrow\Delta a=\frac{a}{2}\)
+ Khi tăng S1S2 một lượng 2\(\Delta\)a thì M là sáng bậc k nên: \(x_M=k\frac{\lambda D}{a+2\Delta a}=2,5\frac{\lambda D}{a}\left(4\right)\)
+ Từ (1) và (4) \(\Rightarrow\) k = 5. Vậy tại M lúc này là vân sáng bậc 5.

Số vân sáng quan sát được là
\(N_s = N_{s1}+ N_{s2}-N_{trung nhau} =17.\)
Số vân sáng của \(\lambda_1\) trên trường giao thoa L là
\(N_{s1}= 2.[\frac{L}{2i_1}]+1 = 9.\)
=> \(N_{s2}= N_s-N_{s1}-N_{trung nhau} = 17-9+3=11.\)
Chọn C
Khi dời màn ra xa thêm 0,3m thì khoảng vân tăng thêm 0,09mm thêm tức là :