Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để đường thẳng (d) vuông góc với đường thẳng ![]() thì 2(3m + 2) = -1 hay:
thì 2(3m + 2) = -1 hay:
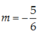
Chọn B.

Xét ptr hoành độ của `(d)` và `(P)` có:
`(m-1)x^2+2mx+3m-1=2x+m`
`<=>(m-1)x^2+2(m-1)x+2m-1=0` `(1)`
`(d)` tiếp xúc `(P)<=>` Ptr `(1)` có nghiệm kép
`<=>{(a \ne 0),(\Delta'=0):}`
`<=>{(m-1 \ne 0),((m-1)^2-(m-1)(2m-1)=0):}`
`<=>{(m \ne 1),(-m(m-1)=0):}`
`<=>m=0`
`->B`
Phương trình hoành độ giao điểm : \(m-1x2+2mx+3m-1=2x+m\)
\(\Leftrightarrow m-1x2+2m-1x+2m-1=0\)
Để d tiếp xúc với P khi và chỉ khi phương trình có nghiệm kép
\(\Leftrightarrow m-1\ne0\Delta'=m-15-m-12m-1=-mm-1=0\) \(\Leftrightarrow m\ne1m=0m=1\Leftrightarrow m=0\)
\(\Rightarrow\) chọn \(B\)

Xét pt hoành độ gđ của (P) và (d) có:
\(x^2-4mx+3m^2+1=2x+3m-2\)
\(\Leftrightarrow x^2-2x\left(2m+1\right)+3m^2-3m+3=0\) (1)
Để (P) và (d) cắt nhau tại hai điểm M;N khi pt (1) có hai nghiệm pb
\(\Leftrightarrow\Delta>0\Leftrightarrow m^2+7m-2>0\Leftrightarrow\left[{}\begin{matrix}m>\dfrac{-7+\sqrt{57}}{2}\\m< \dfrac{-7-\sqrt{57}}{2}\end{matrix}\right.\)
Gọi \(M\left(x_1;2x_1+3m-2\right);N\left(x_2;2x_2+3m-2\right)\) là hai giao điểm của (P) và (d)
\(\Rightarrow\overrightarrow{AM}\left(x_1;2x_1-2\right);\overrightarrow{AN}\left(x_2;2x_2-2\right)\)
(CT tính nhanh diện tích) \(S_{AMN}=\dfrac{1}{2}\left|x_1\left(2x_2-2\right)-x_2\left(2x_1-2\right)\right|\)\(=\dfrac{1}{2}\left|-2x_1+2x_2\right|=\left|x_2-x_1\right|=4\)
\(\Rightarrow\left(x_2-x_1\right)^2=16\)
\(\Leftrightarrow\left(x_2+x_1\right)^2-4x_1x_2=16\)\(\Leftrightarrow\left(4m+2\right)^2-4\left(3m^2-3m+3\right)=16\)
\(\Leftrightarrow4m^2+28m-24=0\)\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{-7+\sqrt{73}}{2}\\m=\dfrac{-7-\sqrt{73}}{2}\end{matrix}\right.\)(tm)
Vậy...

Phương trình hoành độ giao điểm:
\(3x^2-x-5=mx-1\Rightarrow3x^2-\left(m+1\right)x-4=0\)
\(ac=-12< 0\Rightarrow\) phương trình luôn có 2 nghiệm hay (d) luôn cắt (P) tại 2 điểm phân biệt
Theo định lý Viet: \(x_A+x_B=\frac{m+1}{3}\)
\(\Rightarrow y_A+y_B=mx_A-1+mx_B-1=m\left(x_A+x_B\right)-2=\frac{m^2+m-6}{3}\)
Mà tọa độ trung điểm I của AB có dạng: \(\left\{{}\begin{matrix}x_I=\frac{x_A+x_B}{2}=\frac{m+1}{6}\\y_I=\frac{y_A+y_B}{2}=\frac{m^2+m-6}{6}\end{matrix}\right.\)
\(\Rightarrow\frac{m^2+m-6}{6}=\frac{m+1}{6}-1\)
\(\Rightarrow m^2=1\Rightarrow\left[{}\begin{matrix}m=1\\m=-1\end{matrix}\right.\)

Xét hệ phương trình m − 2 x + m − 6 y = − m + 1 m − 4 x + 2 m − 3 y = m − 5 có định thức cấp hai là
D = m − 2 m − 6 m − 4 2 m − 3 = m − 2 . 2 m − 3 − m − 4 . m − 6
= m 2 + 3 m − 18 = m − 3 m + 6
Để hai đường thẳng cắt nhau thì hệ phương trình có nghiệm duy nhất
⟺ D ≠ 0 ⟺ m ≠ 3 m ≠ − 6
ĐÁP ÁN C
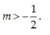
Đáp án B