Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

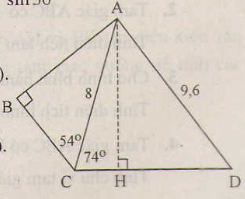
a) Xét tam giác ABC vuông tại B có: AB=AC.sinC=8.sin540≈6,472(cm)AB=AC.sinC=8.sin540≈6,472(cm)
b) Vẽ CD. Xét tam giác ACH có: AH=AC.sinC=8.sin740≈7,690(cm)AH=AC.sinC=8.sin740≈7,690(cm)
Xét tam giác AHD vuông tại H có: sinD=AHAD≈7,6909,6≈0,8010⇒ˆD=530sinD=AHAD≈7,6909,6≈0,8010⇒D^=530
Nhận xét: Để tính được số đo của góc D, ta đã vẽ AH ⊥ CD. Mục đích của việc vẽ đường phụ này là để tạo ra tam giác vuông biết độ dài hai cạnh và có góc D là một góc nhọn của nó. Từ đó tính được một tỉ số lượng giác của góc D rồi suy ra số đo của góc D.

Vì ΔABH vuông tại H(gt)
Mà: \(\widehat{ABC}=45\left(gt\right)\)
=>ΔABH vuông cân tại H
=>BH=AH=8cm
Xét ΔAHC vuông tại H(gt)
=> \(AC^2=AH^2+HC^2\) (theo đl pytago)
=>\(AC^2=8^2+25^2=289\)
=>AC=17cm

a) trong tứ giác EDCB có 2 góc BEC = góc BDC = 90 cùng nhìn 1 cung chứa góc
nên EDCB là tứ giác nội tiếp => góc DEB + góc C = 180 , mà DEB + AED = 180 ( kề bù ) nên góc ACB=AED ( ĐPCM)
b) kéo dài AO tại H,Gọi K là giao điểm của AO và ED, vì B,H,C,A là các thuộc (O) tứ giác BHCA là tứ giác nội tiếp => góc ABC = góc AHC
cmtt như câu a) góc ADE = góc ABC
=> AHC =ADE => xét 2 tam giác đồng dạng AKD và AHC (g.g)
=> góc ACH = góc AKD . Mà ACH = 90 ( AH là đường kính , C thuộc (O) )
=> góc AKD = 90 => AO vuông tại ED ( đpcm)

Vì: CHu vi hcn ABCD là 170
hay: (AB+AD).2=170
=>AB+AD=85
Có:\(\begin{cases}AB+AD=85\\AB-AD=35\end{cases}\)\(\Leftrightarrow\begin{cases}AB=85-AD\\85-AD-AD=35\end{cases}\)\(\Leftrightarrow\begin{cases}AB=85-AD\\-2AD=-50\end{cases}\)
\(\Leftrightarrow\begin{cases}AB=85-25=60\\AD=25\end{cases}\)
Theo đề ra ta có
(+) AB - AD =35 (1)
(+) AB+AD+BC+CD=170
=> (AB+AD)+(BC+CD)=170
=> 2(AB+AD)=170
=> AB+AD=85 (2)
Cộng (1) và (2) Ta có
(AB+AD)+(AB - AD )=85+35
=> 2AB=120
=> AB=60
=> AD=25
=> \(S_{ABCD}=60.26=1500\left(cm^2\right)\)
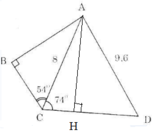
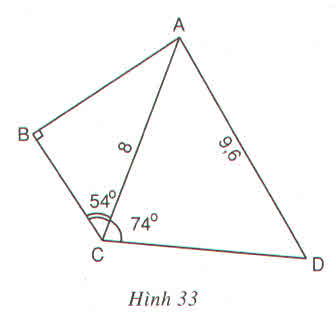




AB = AC.sinC = 8.sin54o = 6,47 (cm)