
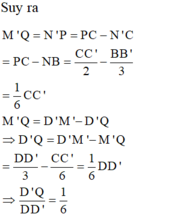
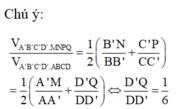
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


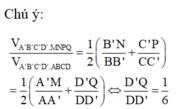

A B C D A' B' C' D' I J
a) Có AA' // DD' và AB//DC nên \(\left(Ax,By\right)\) // \(\left(C_z,D_t\right)\).
b) Do \(\left(Ax,By\right)\) // \(\left(C_z,D_t\right)\) và \(\left(\beta\right)\cap\left(AA'B'B\right)=A'B'\) và \(\left(\beta\right)\cap\left(CC'D'D\right)=C'D'\) nên \(A'B'\) // \(C'D'\).
Chứng minh tương tự B'C'//D'A'.
Do đó tứ giác A'B'C'D' là hình bình hành và J là trung điểm của A'C'.
Suy ra: IJ là đường trung bình của hình thang A'C'CA nên IJ // AA'.
c) Tương tự IJ là đường trung bình của hình thang B'D'DB \(IJ=\dfrac{\left(B'B+DD'\right)}{2}\).
Theo câu b IJ là đường trung bình của hình thang A'C'CA nên \(IJ=\dfrac{\left(AA'+CC'\right)}{2}\).
Suy ra: \(BB'+DD'=AA'+CC'\) hay \(DD'=a+c-b\).

TenAnh1
TenAnh1
A = (-0.14, -7.4)
A = (-0.14, -7.4)
A = (-0.14, -7.4)
B = (14.46, -7.36)
B = (14.46, -7.36)
B = (14.46, -7.36)
C = (-3.74, -5.6)
C = (-3.74, -5.6)
C = (-3.74, -5.6)
D = (11.62, -5.6)
D = (11.62, -5.6)
D = (11.62, -5.6)
E = (-3.34, -5.86)
E = (-3.34, -5.86)
E = (-3.34, -5.86)
F = (12.02, -5.86)
F = (12.02, -5.86)
F = (12.02, -5.86)
G = (-3.7, -5.88)
G = (-3.7, -5.88)
G = (-3.7, -5.88)
H = (11.66, -5.88)
H = (11.66, -5.88)
H = (11.66, -5.88)
a) Các véctơ cùng phương với là:
,
,
,
,
,
,
.
b) Các véctơ cùng hướng với là:
,
,
.
c) Các véctơ ngược hướng với là:
,
,
,
.

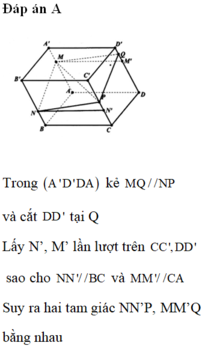
a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:

3.
\(SA\perp\left(ABC\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABC)
\(AB=\sqrt{AC^2+BC^2}=a\sqrt{3}\)
\(tan\widehat{SBA}=\frac{SA}{AB}=\frac{1}{\sqrt{3}}\Rightarrow\widehat{SBA}=30^0\)
4.
\(f'\left(x\right)=\frac{\left(x^2+3\right)'}{2\sqrt{x^2+3}}=\frac{x}{\sqrt{x^2+3}}\) \(\Rightarrow\left\{{}\begin{matrix}f\left(1\right)=2\\f'\left(1\right)=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow S=2+4.\frac{1}{2}=4\)
5.
Hàm \(y=\frac{3}{x^2+2}\) xác định và liên tục trên R
6.
\(\left\{{}\begin{matrix}k_1=f'\left(2\right)\\k_2=g'\left(2\right)\\k_3=\frac{f'\left(2\right).g\left(2\right)-g'\left(2\right).f\left(2\right)}{g^2\left(2\right)}\end{matrix}\right.\) \(\Rightarrow k_3=\frac{k_1.g\left(2\right)-k_2.f\left(2\right)}{g^2\left(2\right)}\Rightarrow\frac{1}{2}=\frac{g\left(2\right)-f\left(2\right)}{g^2\left(2\right)}\)
\(\Leftrightarrow g^2\left(2\right)=2g\left(2\right)-2f\left(2\right)\)
\(\Leftrightarrow1-2f\left(2\right)=\left[g\left(2\right)-1\right]^2\ge0\)
\(\Rightarrow2f\left(2\right)\le1\Rightarrow f\left(2\right)\le\frac{1}{2}\)
1.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=BC\)
\(BC=\sqrt{AC^2-AB^2}=a\)
2.
Qua S kẻ đường thẳng d song song AD
Kéo dài AM cắt d tại E \(\Rightarrow SADE\) là hình chữ nhật
\(\Rightarrow DE//SA\Rightarrow ED\perp\left(ABCD\right)\)
\(SBCE\) cũng là hcn \(\Rightarrow SB//CE\Rightarrow SB//\left(ACM\right)\Rightarrow d\left(SB;\left(ACM\right)\right)=d\left(B;\left(ACM\right)\right)\)
Gọi O là tâm đáy, BD cắt (ACM) tại O, mà \(BO=DO\)
\(\Rightarrow d\left(B;\left(ACM\right)\right)=d\left(D;\left(ACM\right)\right)\)
\(\left\{{}\begin{matrix}AC\perp BD\\AC\perp ED\end{matrix}\right.\) \(\Rightarrow AC\perp\left(BDE\right)\)
Từ D kẻ \(DH\perp OE\Rightarrow DH\perp\left(ACM\right)\Rightarrow DH=d\left(D;\left(ACM\right)\right)\)
\(BD=a\sqrt{2}\Rightarrow OD=\frac{1}{2}BD=\frac{a\sqrt{2}}{2}\) ; \(ED=SA=2a\)
\(\frac{1}{DH^2}=\frac{1}{DO^2}+\frac{1}{ED^2}=\frac{9}{4a^2}\Rightarrow DH=\frac{2a}{3}\)

Lấy điểm O cố định rồi đặt \(\overrightarrow{OA_1}=\overrightarrow{a_1};\overrightarrow{OB_1}=\overrightarrow{b_1};\overrightarrow{OC_1}=\overrightarrow{c_1};\overrightarrow{OD_1}=\overrightarrow{d_1}\)
Điều kiện cần và đủ để tứ giác \(A_1B_1C_1D_1\) là hình bình hành là :
\(\overrightarrow{a_1}+\overrightarrow{c_1}=\overrightarrow{b_1}+\overrightarrow{d_1}\) (1)
\(\overrightarrow{a}+\overrightarrow{c}=\overrightarrow{b}+\overrightarrow{d}\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
<=> Tứ giác ABCD là hình bình hành