Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
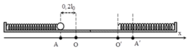
Ta có thể chia nửa chu kì chuyển động của m thành các giai sau:
+ Giai đoạn 1: vật dao động điều hòa từ biên đến vị trí cân bằng O.
Tần số góc của dao động trong giai đoạn này ω = k m → T = 2 π m k
+ Vật đi từ biên A đến vị trí cân bằng O tương ứng với khoảng thời gian t 1 = T 4 = π 2 m k
→ Khi đến O tốc độ của vật là v 0 = ω A = k m 0 , 2 l 0
+ Giai đoạn 2: vật chuyển động thẳng đều từ O đến O’.
Chuyển động trong giai đoạn này được xem là thẳng đều với vận tốc v 0 , vậy thời gian để vật chuyển động trong quãng đường này là t 2 = l 0 v 0 = 5 m k
+ Giai đoạn 3: vật dao động điều hòa từ vị trí cân bằng O′ đến biên A′.
Vật đi từ vị trí cân bằng O′ đến biên A′ tương ứng với khoảng thời gian t 1 = T 4 = π 2 m k
→ Vậy chu kì chuyển động của vật m là: Γ = 2 t 2 + t 2 + t 3 = 2 π + 10 m k

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B

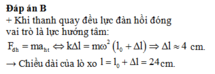




Đáp án B