
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Từ thông cực đại: \(\phi_0=N.B.S = 2000.10^{-2}.0,2^2=0,8Wb\)
t = 0 chọn lúc mặt phẳng khung dây vuông góc với đường sức, có nghĩa véc tơ pháp tuyến của khung trùng với đường sức
\(\Rightarrow \varphi =0\)
Vậy biểu thức từ thông: \(\phi=0,8.\cos(100\pi t)(Wb)\)

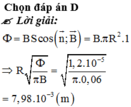
Ta có qua diện tích giới hạn bởi khung dây:
![]()
Suy ra bán kính vòng dây:
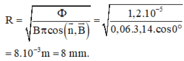

Ta có qua diện tích giới hạn bởi khung dây:
\(\Phi=BScos\left(\overrightarrow{n},\overrightarrow{B}\right)=B\pi R^2cos\left(\overrightarrow{n},\overrightarrow{B}\right)\)
Suy ra bán kính vòng dây:
\(R=\sqrt{\dfrac{\Phi}{B\pi cos\left(\overrightarrow{n},\overrightarrow{B}\right)}}=\sqrt{\dfrac{1,2.10^{-5}}{0,06.3,14.cos0^o}}\)
\(=8.10^{-3}m=8mm\)

Ta có: ϕ = BScos( n , ⇀ B ⇀ ) = BπR 2 cos( n , ⇀ B ⇀ )
=> R = ϕ Bπcos ( n ⇀ , B ⇀ ) = 8 . 10 - 3 m = 8 mm.