Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Th1 : Số cách chọn ra 1 nhà toán học nam, 1 nhà toán học nữ, 1 nhà vật lý nam : 5.3.4 = 60
Th2 : Số cách chọn ra 2 nhà toán học nữ, 1 nhà vật lý nam : C 3 2 C 4 1 = 12
Th3 : Số cách chọn ra 1 nhà toán học nữ, 2 nhà vật lý nam : C 3 1 C 4 2 = 18
Vậy có số cách chọn là : 90

Số học sinh nữ bằng 5/3 học sinh nam nghĩa là số học sinh nam bằng 3/8 số học sinh cả lớp.
Số học sinh nữ bằng 7 lần số học sinh nam nghĩa là số học sinh nam bằng 1/8 số học sinh cả lớp.
Phân số chỉ số 10 học sinh nam :
3/8 - 1/8 = 1/4 học sinh cả lớp (hay 10 học sinh nam)
Số học sinh cả lớp:
10 : 1/4 = 40 (học sinh)
Số học sinh nam:
40 x 3/8 = 15 (học sinh)
Số học sinh nữ:
40 - 15 = 25 (học sinh)
DS: Nam: 15 học sinh
Nữ: 25 học sinh

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

ta tính \(y'=6x^2+a-12\)
để hàm số vừa có cực đại và cực tiểu thì \(y'=0\) hai nghiệm phân biệt suy ra \(6x^2+a-12=0\Leftrightarrow6x^2=12-a\) (*)
để (*) có 2 nghiệm phân biệt thì \(12-a>0\Leftrightarrow a<12\)
vậy với a<12 thì hàm số có cực đại và cực tiểu
gọi \(x_1;x_2\) là cực đại và cực tiểu của hàm số
suy ra \(x_{1,2}=\pm\sqrt{\frac{12-a}{6}}\) ta thay vào hàm số suy ra đc \(y_{1,2}\) suy ra \(I\left(x_1;y_1\right);A\left(x_2;y_2\right)\)
sử dụng công thức tính khoảng cách
pt đường thẳng y có dạng x=0
ta có \(d\left(I;y\right)=\frac{\left|x_1\right|}{\sqrt{1}}\); \(d\left(A;y\right)=\frac{\left|x_2\right|}{\sqrt{1}}\)
\(d\left(I,y\right)=d\left(A,y\right)\) giải pt ta tìm ra đc a

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

2.
Gọi quãng đường cần tìm là s.---> vận tốc Xuân= s/12,
--> vận tốc Hạ=s/10
thời gian Xuân gặp Hạ: 50/(s/12)= (s-50)/(s/10)
50x12/s= (s-50)x10/s
50x12=10s-500
---> s = (500+50x12)/10= 110
quãng đường giữa nhà hai bạn là 110m
4.
Khi ngược dòng 1 giờ ta đi được số phần quãng sông là:
1 : 8 = 1/8 (quãng sông)
Khi xuôi dòng 1 giờ ta đi được số phần quãng sông là:
1 : 4 = 1/4 (quãng sông)
Bèo trôi theo ta về 1 giờ trôi được số phần quãng sông là:
(1/4 - 1/8) : 2 = 1/16 (quãng sông)
Bèo trôi theo ta về cập bến sau số giờ là:
1 : 1/16 = 16 (giờ)
Đ/s: 16 giờ

Nếu số bạn nam là a và số bạn nữ là b.
Mỗi bạn nam có a-1 bạn nam (trừ ra chính bạn đó), và b bạn nữ. Theo bài ra thì a-1 = b.
Mỗi bạn nữ có a bạn nam và b-1 bạn nữ (trừ ra chính bạn nữ đó). Theo bài ra ta có a = 2(b-1).
Vậy ta có:
a - 1 = b
a = 2(b - 1)
Suy ra a = 4, b = 3
Nếu số bạn nam là a và số bạn nữ là b.
Mỗi bạn nam có a-1 bạn nam (trừ ra chính bạn đó), và b bạn nữ. Theo bài ra thì a-1 = b.
Mỗi bạn nữ có a bạn nam và b-1 bạn nữ (trừ ra chính bạn nữ đó). Theo bài ra ta có a = 2(b-1).
Vậy ta có:
a - 1 = b
a = 2(b - 1)
Suy ra a = 4, b = 3.
Vậy nhóm học sinh có 4 bạn nam và 3 bạn nữ.
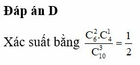

Chọn C.
Số cách chọn 4 nhà khoa học mà có đủ cả ba lĩnh vực là
Số cách chọn 4 nhà khoa học nam mà có đủ cả ba lĩnh vực là
Số cách chọn 4 nhà khoa học nữ mà có đủ cả ba lĩnh vực là
Vậy số cách lập một ban thư kĩ thỏa mãn yêu cầu là: