Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận tóc của chuyển động là:
\(v=s'=12t-3t^2\)
Ta có \(v'=12-6t\)
\(v'=0\) khi t = 2 và \(v'\) đổi dấu từ dương sang âm khi đi qua t=2. Vậy \(v\) đạt giá trị lớn nhất khi t = 2.

s = 6 t 2 − t 3 , t > 0
Vận tốc chuyển động là v = s’ , tức là v = 12t – 3 t 2
Ta có: v’ = 12 – 6t
v’ = 0 ⇔ t = 2
Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+ ∞ ).
Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó max V = V C Đ = v(2) = 12(m/s).

s = 6 t 2 – t 3 , t > 0
Vận tốc chuyển động là v = s’ , tức là v = 12t – 3 t 2
Ta có: v’ = 12 – 6t
v’ = 0 ⇔ t = 2
Hàm số v đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+ ∞ ).
Vận tốc đạt giá trị lớn nhất khi t = 2. Khi đó max V = V CD = v(2) = 12(m/s).

3.
\(x^2+4y^2=x^2+8.\frac{y^2}{2}\ge9\sqrt[9]{\frac{x^2y^{16}}{2^8}}\)
\(\Rightarrow\sqrt{x^2+4y^2}\ge\sqrt{9\sqrt[9]{\frac{x^2y^{16}}{2^8}}}=3\sqrt[9]{\frac{xy^8}{2^4}}\)
\(\Rightarrow x+\sqrt{x^2+4y^2}\ge x+3\sqrt[9]{\frac{xy^8}{2^4}}\ge4\sqrt[4]{x\sqrt[3]{\frac{xy^8}{2^4}}}=4\sqrt[12]{\frac{x^4y^8}{2^4}}=4\sqrt[3]{\frac{xy^2}{2}}\)
\(\Rightarrow\left(x+\sqrt{x^2+4y^2}\right)^3\ge\left(4\sqrt[3]{\frac{xy^2}{2}}\right)^3=32xy^2\)
\(\Rightarrow P\le\frac{4xy^2}{32xy^2}=\frac{1}{8}\)
\(P_{max}=8\) khi \(y=x\sqrt{2}\)
4.
\(y'=x^2+2\left(m+1\right)x+4\) (1)
Để hàm số nghịch biến trên 1 đoạn có độ dài bằng \(2\sqrt{5}\)
\(\Leftrightarrow\left(1\right)\) có 2 nghiệm pb thỏa mãn \(\left|x_2-x_1\right|=2\sqrt{5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m+1\right)^2-4>0\\\left(x_2-x_1\right)^2=20\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m^2+2m-3>0\\\left(x_1+x_2\right)^2-4x_1x_2=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>1\\m< -3\end{matrix}\right.\\4\left(m+1\right)^2-16=20\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=2\\m=-4\end{matrix}\right.\)
\(\Rightarrow\sum m=-2\)
5.
Pt đoạn chắn: \(\frac{x}{2}+\frac{y}{-3}+\frac{z}{4}=1\Leftrightarrow6x-4y+3z+12=0\)
Mặt phẳng (MNP) nhận \(\left(6;-4;3\right)\) là 1 vtpt
1.
\(v\left(t\right)=s'\left(t\right)=-3t^2+12t+17=-3\left(t-2\right)^2+29\le29\)
\(\Rightarrow v\left(t\right)_{max}=29\) khi \(t=2\left(s\right)\)
2.
E là trung điểm AD \(\Rightarrow ABCE\) là hình vuông
Gọi O là giao điểm AC và BE, qua O kẻ đường thẳng song song SA cắt SC tại I
\(\Rightarrow\) I là tâm mặt cầu ngoại tiếp S.ABCE
\(\Rightarrow R=IC=\frac{SC}{2}\)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\) \(\Rightarrow SC=\sqrt{SA^2+AC^2}=2a\)
\(\Rightarrow R=\frac{AC}{2}=a\)

a) Ta có:
v(t) = s’(t) = t3 – 3t2 + t – 3
a(t) = s’’(t) = 3t2 – 6t + 1
Do đó: v(2) = -5; a(2) = 1
b) v(t) = 0 ⇔ t3 – 3t2 + t – 3
⇔ t = 3
Vậy t = 3
Theo ý nghĩa cơ học của đạo hàm ta có:
v(t)=s'(t)=t3-3t2+t-3
v(2)=23-3.22+2-3=-5 (m/s)
a(t)=v'(t)=s''(t)=3t2-6t+1
a(2)=3.22-6.2+1=1 (m/s2)
v(t)=t3-3t2+t-3=0
(t-3)(t1+1)=0 t = 3
Vậy thời điểm to=3s thì vận tốc bằng 0.

lưa ý pt \(x^2=m^2-m+1\)có nghiệm với x phải #0 vì nếu = 0 thì trùng => sai
nhưng nghiệm \(\left(+,-\right)\sqrt{m^2-m+1}\)luôn #0 rồi khỏi lo
\(y'=6x^2-6\left(m+1\right)x+6m\)
ta có y/y'=\(\left(3m-1\right)x+m^3+m^2+m\)
suy ra y= \(\left(3m-1\right)x+m^3+m^2+m\)là pt của dường thẳng đi qua A và B
de-ta \(=9\left(m+1\right)^2-36m\)
y' có 2 \(n_o\)phân biệt khi m#1
hai hoành độ của hai điểm cực trị là :
\(X=\dfrac{-b\left(+,-\right)\sqrt{deta}}{a}=\)
\(\left[{}\begin{matrix}\dfrac{m+3}{2}\\\dfrac{3m-1}{2}\end{matrix}\right.\)<=>y=\(\left[{}\begin{matrix}2m^3+5m^2+10m+3\\2m^3+11m^2+4m+1\end{matrix}\right.\)(tìm y bằng cách thế x vào pt đường thẳng )
khoảng cách giữa hai điểm AB =\(\sqrt{2}\)
ta có pt : \(2=\left(\dfrac{m+3}{2}-\dfrac{3m-1}{2}\right)^2+\left(2m^3+5m^2+10m-3-\left(2m^3+11m^2-4m+1\right)\right)^2\)
lại sai chỗ nào rồi 0 ra nghiệm , cậu tính lại thử , cách giả là như vậy
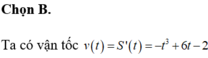
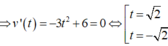

Chọn A.
Vận tốc của chuyển động là v = s' tức là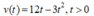
Bảng biến thiên:
Hàm số v(t) đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+∞)
⇔ Max v(t) = 12 khi t = 2.
Vận tốc đạt giá trị lớn nhất bằng 12 khi t = 2(s).