Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Tần số của mạch dao động LC được tính theo công thức:
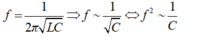
- Khi C = C1 thì:
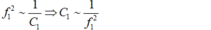
- Khi C = C1 + C2 thì:
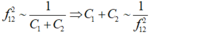
- Từ đó suy ra:
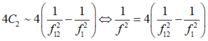
- Thay số vào ta tính được tần số khi C = 4C2 là f = 20MHz

Tần số dao động riêng: \(f=\frac{1}{2\pi\sqrt{LC}}\Rightarrow\frac{1}{f^2}=k.C\)(Vì chỉ thay đổi C nên ta biểu diễn f theo C, k là một hệ số nào đó)
Suy ra:
\(\frac{1}{f_1^2}=k.C_1\)
\(\frac{1}{f_2^2}=k.C_2\)
Ta cần tìm:
\(\frac{1}{f^2}=k\left(C_1+C_2\right)\Rightarrow\frac{1}{f^2}=kC_1+kC_2\)
\(\Rightarrow\frac{1}{f^2}=\frac{1}{f_1^2}+\frac{1}{f_2^2}\)
Thay số ta đc f = 35Hz


Xem t = 0 là lúc cả hai mạch bắt đầu dao động
Phương trình hiệu điện thế trên 2 tụ C1 và C2 lần lượt có dạng
\(\begin{cases}u_1=12cos\left(\omega t\right)\left(V\right)\\u_2=6cos\left(\omega t\right)\left(V\right)\end{cases}\)
Độ chênh lệch Hiệu điện thế: \(\Delta u=u_1-u_2=6cos\left(\omega t\right)\left(V\right)\)
\(u_1-u_2=6cos\left(\omega t\right)=\pm3\Rightarrow cos\left(\omega t\right)=\pm0,5\Rightarrow cos\left(\frac{2\pi}{T}t\right)=\pm0,5\)
\(\Rightarrow\Delta t_{min}=\frac{T}{6}=\frac{10^{-6}}{3}s\)

Tần số: \(f=\dfrac{1}{2\pi\sqrt {LC}}\Rightarrow f^2=\dfrac{a}{C}\) (a là 1 hằng số nào đó, do bài này f chỉ phụ thuộc vào C)
\(\Rightarrow f_1^2=\dfrac{a}{C_1}\)
\(f_2^2=\dfrac{a}{C_2}\)
Cần tìm: \(\Rightarrow f^2=\dfrac{a}{C}=a.(\dfrac{1}{C_1}+\dfrac{1}{C_2})=f_1^2+f_2^2\)
\(\Rightarrow f=\sqrt{30^2+40^2}=50(Hz)\)
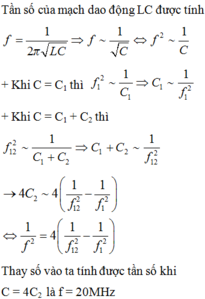

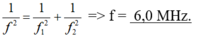

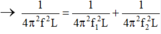
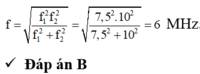
Tần số của mạch dao động LC được tính theo công thức
Thay số vào ta tính được tần số khi C = 4C2 là f = 20MHz
Đáp án A