Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mặt phẳng ( β ) song song với trục Oy và vuông góc với mặt phẳng ( α ):
2x – y + 3z + 4 = 0, do đó hai vecto có giá song song hoặc nằm trên ( β ) là: j → = (0; 1; 0) và n α → = (2; −1; 3)
Suy ra ( β ) có vecto pháp tuyến là n β → = j → ∧ n α → = (3; 0; −2)
Mặt phẳng ( β ) đi qua điểm M(2; -1; 2) có vecto pháp tuyến là: n β → = (3; 0; −2)
Vậy phương trình của ( β ) là: 3(x – 2) – 2(z – 2) = 0 hay 3x – 2z – 2 = 0

Mặt phẳng ( α ) song song với mặt phẳng ( β ): x + y + 2z – 7 = 0
Vậy phương trình của ( α ) có dạng : x + y + 2z + D = 0
( α ) đi qua gốc tọa độ O(0; 0; 0) suy ra D = 0.
Vậy phương trình của ( α ) là x + y + 2z = 0.

Vectơ →nn→(2 ; -1 ; 3) là vectơ pháp tuyến của mặt phẳng ( β) .
Vì (α) // ( β) nên →nn→ cũng là vectơ pháp tuyến của mặt phẳng (α) .
Phương trình mặt phẳng (α) có dạng:
2(x - 2) - (y + 1) + 3(z - 2) = 0
hay 2x - y + 3z -11 = 0.

Đáp án B.
Phương pháp: Mặt phẳng α đi qua M và nhận
![]()
Cách giải: Mặt phẳng α đi qua M và nhận là 1 VTPT nên có phương trình:
![]()
nên có phương trình:
![]()
![]()

Đáp án B.
Phương pháp: Mặt phẳng α đi qua M
![]()
Cách giải: Mặt phẳng α đi qua M và
![]()
nên có phương trình:
![]()
![]()
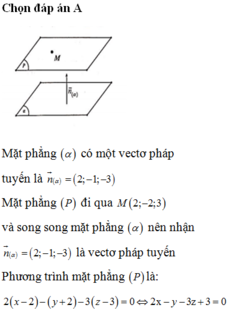

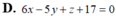


Vì mặt phẳng (α) song song với mặt phẳng ( β) : 2x – y + 3z + 4 = 0 nên phương trình của mp(α) có dạng 2x – y + 3z + D = 0
Vì M(2; -1; 2) ∈ mp(α) nên 4 + 1 + 6 + D = 0 <=> D = -11
Vậy phương trình của mp(α) là: 2x – y + 3z - 11= 0