Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
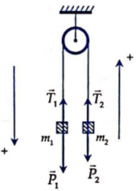
Bỏ qua khối lượng ròng rọc: T 1 = T 2 = T
Dây không dãn: a = a 1 = a 2 = a.
Áp dụng định luật II Niu-tơn cho từng vật với chiều dương tương ứng như hình vẽ, ta có:
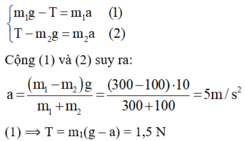
Chú ý: Có thể áp dụng luôn định luật II Niu-tơn cho hệ hai vật với lưu ý chọn trục chung cho cả hai vật hướng dọc theo dây từ vật m 2 sang vật m 1 .
Suy ra ngay:
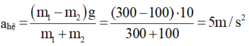
Tuy nhiên để tìm T vẫn phải viết định luật II Niu-tơn cho một trong hai vật.

1.
theo phương pháp tổng hợp hai lực song song cùng chiều
\(F=F_1+F_2=24N\Rightarrow F_2=24-F_1=6N\) và
\(\dfrac{F_1}{F_2}=\dfrac{d_2}{d_1}\)\(\Leftrightarrow\dfrac{18}{6}=\dfrac{d_2}{30-d_2}\Rightarrow d_2=22,5cm\)
2.
. T N P -P
a)
\(sin\alpha=\dfrac{T}{P}\Rightarrow T=m.g.sin\alpha=\)24,5N
b)\(cos\alpha=\dfrac{N}{P}\Rightarrow N=\dfrac{49\sqrt{3}}{2}N\)

a) cơ năng tại vị trí ban đầu của vật
\(W_A=W_{đ_A}+W_{t_A}=\dfrac{1}{2}.m.v_0^2+m.g.h\)=300J
gọi vị trí mà vật đạt độ cao cực đại là B
bảo toàn cơ năng: \(W_A=W_B\)
để \(W_{t_{B_{max}}}\) thì \(W_{đ_B}=0\)
\(\Leftrightarrow300=m.g.h_{max}+0\)
\(\Leftrightarrow h_{max}\)=15m
b) gọi vị trí mà động năng bằng 1/3 lần thế năng là C \(\left(W_{đ_C}=\dfrac{1}{3}W_{t_C}\right)\)hay\(\left(3W_{đ_C}=W_{t_C}\right)\)
bảo toàn cơ năng: \(W_A=W_C\)
\(\Leftrightarrow300=4.W_{đ_C}\)
\(\Leftrightarrow v=\)\(5\sqrt{3}\)m/s
c) s=10cm=0,1m
vị trí tại mặt đất là O (v1 là vận tốc khi chạm đất)
\(W_A=W_O\Leftrightarrow300=\dfrac{1}{2}.m.v_1^2+0\)
\(\Rightarrow v_1=\)\(10\sqrt{3}\)m/s
lực cản của mặt đất tác dụng vào vật làm vật giảm vận tốc (v2=0)
\(A_{F_C}=\dfrac{1}{2}.m.\left(v_2^2-v_1^2\right)\)
\(\Leftrightarrow F_C.s=-100\)
\(\Rightarrow F_C=-1000N\)
lực cản ngược chiều chuyển động

Bạn nhớ viết hoa đầu dòng nhé, và quy tắc bỏ dấu trong văn bản word:
Hướng dẫn:
Cơ năng ban đầu: W1 = mgh
Cơ năng khi chạm đất: W2 = 1/2 mv2
Bảo toàn cơ năng: \(W_1=W_2\Rightarrow v=\sqrt{2gh}\)

chọn hệ trục xOy như hình vẽ ta có
các lực tác dụng lên vật là: \(\overrightarrow{Fms},\overrightarrow{F},\overrightarrow{P},\overrightarrow{N}\)
theo định luật 2 Newton ta có
\(\overrightarrow{F}+\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}=\overrightarrow{a}.m\left(1\right)\)
chiếu phương trình 1 lên trục Oy ta có
-P + N=0
\(\Leftrightarrow\)P=N\(\Rightarrow\)Fms=\(\mu.N=\mu.mg\)
chiếu pt 1 lên trục Ox ta có
F-Fms=am
\(\Rightarrow\)F=am-Fms=a.m-\(\mu mg\)=1,25.10-0,3.4.10=0,5(N)
Vậy ..........
O x y P N Fms F

1.ta có V^2-Vo^2=2as ( vs a=-g vì cđ ném lên) =>s=(-100)/-20=5m
2. viết pt2niuton .chọn chiều hướng nên là chiều+ :<=>P+Fc=ma(pt vecto)
chiếu + =>-p-f=ma <=>-1.05g=a =>a=-10.5
ta có V^2-Vo^2=2as =>s =-Vo^2/2a =>s=4.7619m
vật cđ xuống =>pt2niuron:P+Fc=ma ( chọn chiều + là chiều hướng xuống)
chiếu +:p-f=ma<=>0.95g=a =>a=9.5
V^2-Vo^2=2as =>V=\(\sqrt{2as}\) =>V=9.51

O A B C D E
l=40cm=0,4m
gốc thế năng tại vị trí vân bằng
a) cơ năng tại C
\(W_C=W_{đ_C}+W_{t_C}=0+m.g.AE\)
(AE=\(l-OE\))
\(\Leftrightarrow W_C=m.g.\left(l-l.cos60^0\right)=\)2J
cơ năng tại B
\(W_B=W_{t_B}+W_{đ_B}=m.g.\left(l-l.cos30^0\right)+\dfrac{1}{2}.m.v_B^2\)
\(\Leftrightarrow\)\(W_B=\)\(4-2\sqrt{3}+\dfrac{1}{2}.mv_B^2\)
bảo toàn cơ năng
\(W_B=W_C\)
\(\Rightarrow v_B\approx\)1,71m/s
vật quay tròn quanh tâm O
\(\overrightarrow{T}+\overrightarrow{P}=m.\overrightarrow{a_{ht}}\)
chiếu lên trục Ox phương song song dây, chiều dương hướng vào trong
\(T-m.g.cos30^0=m.\dfrac{v_B^2}{l}\)
\(\Rightarrow T\approx16N\)
b) cơ năng tại vị trí cân bằng
\(W_A=0+\dfrac{1}{2}.m.v^2_A\)
bảo toàn cơ năng: \(W_A=W_C\)
\(\Rightarrow v_A=\)2m/s
lực căng dây lúc này
\(T=P+m.\dfrac{v_B^2}{l}\)=20N
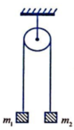
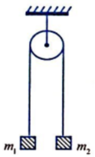

Chọn C.
Bỏ qua khối lượng ròng rọc: T1 = T2 = T
Dây không dãn: a = a1 = a2 = a.
Áp dụng định luật II Niu-tơn cho từng vật với chiều dương tương ứng như hình vẽ, ta có: