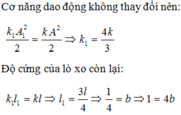Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Sau khi giữ vật tại điểm chính giữa, vật sẽ dao động với lò xo có độ cứng k 1 = 2 k . Con lắc lò xo mới có chiều dài tự nhiên lo/2. Tại thời điểm giữ lò xo chiều dài con lắc này là x=A/2 tức là lò xo này đã giãn A/2.
Hay ly độ và vận tốc của vật lúc này là x = A/2 và v = 0 (do tại vị trí biên)
Suy ta, biên độ dao động sẽ là
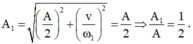 .
.

Hướng dẫn:
+ Tại vị trí x = Δl = 0,5A động năng của vật bằng 3 lần thế năng: E d = 0 , 75 E và E t = 0 , 25 E .
Khi ta giữ điểm chính giữa của lò xo thì một nửa thế năng ban đầu mất đi theo phần lò xo không tham gia vào dao động của hệ lúc sau, động năng vẫn không đổi.
→ E′ = 0,75E + 0,125E = 0,875E.
+ Với k′ = 2k → F d h m a x F ' d h m a x = k k ' k ' E k E ' = 2 7
Đáp án B

Chọn A
Tại thời điểm cố định lò xo ta có E d = n E t E d + E t = E → E t = E n + 1 E d = n E n + 1
+ Vì thế năng đàn hồi của lò xo phân bố đều trên mỗi đơn vị chiều dài, do vậy thế năng của hệ dao động mới là E ' t = E t m = E m n + 1
+ Cơ năng của hệ dao động mới: E ' = E ' t + E ' d = E m n + 1 + n E n + 1 = 1 2 k ' A ' 2
Trong đó k′ = mk là độ cứng của phần lò xo tham gia vào dao động của vật lúc sau.
→ Biến đổi toán học ta thu được tỉ số A ' A = m n + 1 2 m n + 1

Tại thời điểm giữ lò xo thì: \(W_{d}=W_{t}=\dfrac{W}{2}\)
Cố định 1 điểm chính giữa lò xo thì thế năng giảm đi 1 nửa
\(\Rightarrow W_{t'}=\dfrac{W_t}{2}=\dfrac{W}{4};W_{đ}=\dfrac{W}{2}\Rightarrow W'=\dfrac{3W}{4}\)
Có: \(k'=2k\Rightarrow \dfrac{3}{4}.kA^{2}=k'A'^{2}\)
\(\Rightarrow \dfrac{A}{A'}=\dfrac{4}{\sqrt{6}}\)