Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: A=1>\(\dfrac{5}{x}\)> 0(vì x>5)(1)
B= \(\dfrac{5}{x}\)+1=\(\dfrac{5+x}{x}\)>1(2)
C= \(\dfrac{5}{x}\)-1=\(\dfrac{5-x}{x}\) < 0(3)
D=\(\dfrac{x}{5}\)>1(4)
Từ(1),(2),(3),(4):
Ta thấy đáp án C là đáp án duy nhất bé hơn không nên đáp án C= \(\dfrac{5}{x}\)-1 là đáp án có số nhỏ nhất.
Bài 1a)
Áp dụng bất đẳng thức Cô-si cho từng cặp ta có
\(\left\{\begin{matrix}a+b\ge2\sqrt{ab}\\b+c\ge2\sqrt{bc}\\c+a\ge2\sqrt{ac}\end{matrix}\right.\)
\(=>\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ac}\)
\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\sqrt{\left(abc\right)^2}\)
\(=>\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8abc\) ( điều phải chứng minh )
Bài 1b)
Áp dụng bất đẳng thức Cô-si bộ 3 số cho từng cặp ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\a^2+b^2+c^2\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\left(abc\right)^2}\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9\sqrt[3]{\left(abc\right)^3}\)
\(=>\left(a+b+c\right)\left(a^2+b^2+c^2\right)\ge9abc\) (điều phải chứng minh )
Bài 1c) Ta có
\(\left(1+a\right)\left(1+b\right)\left(1+c\right)\ge\left(1+\sqrt[3]{abc}\right)^3\)
\(=>1+a+b\left(1+a\right)\left(1+c\right)\ge1^3+3.1^2.\sqrt[3]{abc}+3.1.\sqrt[3]{\left(abc\right)^2}+\sqrt[3]{\left(abc\right)^3}\)
\(=>\left(1+a+b+ab\right)\left(1+c\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>1+a+b+ab+c\left(1+a+b+ab\right)\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>1+a+b+ab+c+ca+bc+abc\ge1+3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}+abc\)
\(=>a+b+c+ab+bc+ca\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\)
Áp dụng bất đẳng thức Cô-si bộ 3 số cho vế trái ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\ab+bc+ac\ge3\sqrt[3]{\left(abc\right)^2}\end{matrix}\right.\)
\(=>a+b+c+ab+bc+ac\ge3\sqrt[3]{abc}+3\sqrt[3]{\left(abc\right)^2}\) (điều phải chứng minh )
Bài 2a)
Áp dụng bất đẳng thức Cô-si cho từng cặp ta có
\(\left\{\begin{matrix}\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}.\frac{ca}{b}}=2\sqrt{c^2}=2c\\\frac{ca}{b}+\frac{ab}{c}\ge2\sqrt{\frac{ca}{b}.\frac{ab}{c}}=2\sqrt{a^2}=2a\\\frac{bc}{a}+\frac{ab}{c}\ge2\sqrt{\frac{bc}{a}.\frac{ab}{c}}=2\sqrt{b^2}=2b\end{matrix}\right.\)
\(=>2\left(\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\right)\ge2\left(a+b+c\right)\)
\(=>\frac{bc}{a}+\frac{ca}{b}+\frac{ab}{c}\ge a+b+c\) (điều phải chứng minh )
Bài 2b)
Chứng minh BĐT \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
Áp dụng BĐT Cô-si cho vế trái ta có
\(\left\{\begin{matrix}a+b+c\ge3\sqrt[3]{abc}\\\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\end{matrix}\right.\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\frac{1}{abc}}\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9.\sqrt[3]{\frac{abc}{abc}}\)
\(=>\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\) (điều phải chứng minh )
Ta có \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\ge\frac{3}{2}\)
\(=>\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}+3\ge\frac{3}{2}+3\)
\(=>\frac{a}{b+c}+1+\frac{b}{a+c}+1+\frac{c}{a+b}+1\ge\frac{9}{2}\)
\(=>\frac{a+b+c}{b+c}+\frac{a+b+c}{a+c}+\frac{a+b+c}{a+b}\ge\frac{9}{2}\)
\(=>\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge\frac{9}{2}\)
\(=>2\left(a+b+c\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9\)
Áp dụng BĐT vừa chứng minh \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(=>\left(b+c+a+c+a+b\right)\left(\frac{1}{b+c}+\frac{1}{a+c}+\frac{1}{a+b}\right)\ge9 \) (Điều phải chứng minh )
a: \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\left(\dfrac{1}{x_1-2}-\dfrac{1}{x_2-2}\right):\left(x_1-x_2\right)\)
\(=\dfrac{x_2-2-x_1+2}{\left(x_1-2\right)\left(x_2-2\right)}\cdot\dfrac{1}{x_1-x_2}=\dfrac{-1}{\left(x_1-2\right)\left(x_2-2\right)}\)
Trường hợp 1: \(\left\{{}\begin{matrix}x_1< 2\\x_2< 2\end{matrix}\right.\Leftrightarrow\left(x_1-2\right)\left(x_2-2\right)>0\)
=>\(\dfrac{-1}{\left(x_1-2\right)\left(x_2-2\right)}< 0\)
Do đó: F(x) nghịch biến khi \(x\in\left(-\infty;2\right)\)
TRường hợp 2: \(\left\{{}\begin{matrix}x_1>2\\x_2>2\end{matrix}\right.\Leftrightarrow\left(x_1-2\right)\left(x_2-2\right)>0\)
=>\(\dfrac{-1}{\left(x_1-2\right)\left(x_2-2\right)}< 0\)
Do đó: F(x) nghịch biến khi \(x\in\left(2;+\infty\right)\)
b: \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2-6x_1+5-x_2^2+6x_2-5}{x_1-x_2}=\left(x_1+x_2\right)-6\)
Trường hợp 1: \(\left\{{}\begin{matrix}x_1< 3\\x_2< 3\end{matrix}\right.\Leftrightarrow x_1+x_2-6< 0\)
=>Hàm số nghịch biến khi x<3
Trường hợp 2: \(\left\{{}\begin{matrix}x_1>3\\x_2>3\end{matrix}\right.\Leftrightarrow x_1+x_2-6>0\)
=>Hàm số đồng biến khi x>3
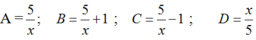
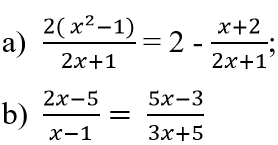
Với mọi x ≠ 0 ta luôn có: - 1 < 0 < 1. Do đó,
Lại có x > 5 ⇒ x2 > 52 (Bình phương hai vế)
⇒
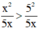(Nhân cả hai vế của bất đẳng thức với 
)
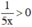Vậy ta có C < A < B và C < A < D nên trong bốn số trên, C là số nhỏ nhất.