Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

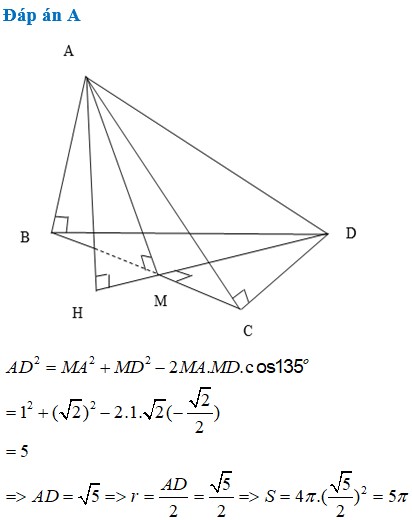
Đáp án C.
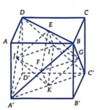
Cho hình lập phương ABCD.A'B'C'D'. Gọi E,F,G,I,J,K là tâm các mặt của nó. Khi đó các đỉnh E,F,G,I,J,K tạo thành hình bát diện đều EFGHIJK.
Đặt A B = a thì E J = A ' B 2 = a 2 2 .
Thể tích của khối bát diện đều có cạnh bằng x được tính bằng công thức V = x 3 2 3 . Áp dụng vào bài toán ta có V E F G Ị K = 1 3 . a 2 2 3 . 2 = a 3 6 .
Vậy tỉ số thể tích cần tìm là a 3 6 a 3 = 1 6 .

Đáp án C
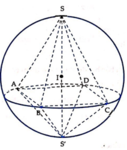
Mặt cầu (S) có tâm I 1 ; 0 ; 2 , bán kính R=3. Nhận xét thấy S, I, S’ thẳng hàng và S S ' ⊥ A B C D . Khi đó S S ' = 2 R = 6 . Ta có:
V H = V S . A B C D + V S ' . A B C D = 1 3 d S ; A B C D . S A B C D + 1 3 d S ' ; A B C D . S A B C D
= 1 3 d S ; A B C D + d S ' ; A B C D . S A B C D = 1 3 S S ' . S A B C D = 2 S A B C D
Từ giả thiết suy ra ABCD là hình vuông, gọi a là cạnh hình vuông đó.
Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng r và ngoại tiếp hình vuông ABCD.
Suy ra 2 r = A C = a 2 ⇒ r = a 2 2 . Từ d I ; P 2 + r 2 = R 2 .
⇔ r = R 2 − d I ; P 2 = 3 2 − 8 3 2 = 17 3 = a 2 2 ⇔ a = 2 17 3 2
Vậy V H = 2 S A B C D = 2 a 2 = 2. 2 17 3 2 2 = 68 9 .


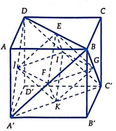
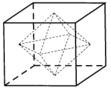
Đáp án C.
Đặt (H) là hình tứ diện đều ABCD, cạnh bằng A. Gọi E ; F ; I ; J lần lượt là tâm của các mặt A B C ; A B D ; A C D ; B C D .
Kí hiệu như hình vẽ.
Ta có M E M C = M F M D = 1 3 ⇒ E F C D = 1 3 ⇒ E F = C D 3 = a 3 .
Vậy tứ diện là tứ diện đều có cạnh bằng a 3 .
Tỉ số thể tích của diện tích toàn phần tứ diện đều và tứ diện đều ABCD là a 3 a 2 = 1 9