Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

_ Thể tích khối lăng trụ :
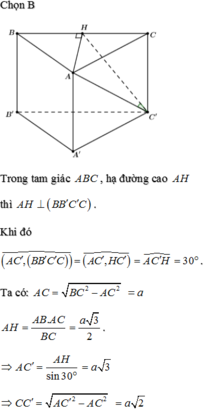
Gọi D là trung điểm của BC ta có : \(BC\perp AD\Rightarrow BC\perp A'D\Rightarrow\widehat{ADA'}=60^0\)
Ta cso \(AA'=AD.\tan\widehat{ADA'}=\frac{3a}{2};S_{ABC}=\frac{a^2\sqrt{3}}{4}\)
Do đó \(V_{ABC.A'B'C'=}S_{ABC}.AA'=\frac{3a^2\sqrt{3}}{8}\)
- Bán kính mặt cầu ngoại tiếp tứ diện GABC :
Ta có I là giao điểm của GH với đường trung trực của AG trong mặt phẳng (AGH)
Gọi E là trung điểm của AG, ta có :
\(R=GI=\frac{GE.GA}{GH}=\frac{GA^2}{2GH}\)
Ta có :
\(GH=\frac{AA'}{3}=\frac{a}{2};AH=\frac{a\sqrt{3}}{3};GA^2=GH^2+AH^2=\frac{7a^2}{12}\)
Do đó \(R=\frac{7a^2}{2.12}.\frac{2}{a}=\frac{7a}{12}\)

Đáp án B
Trong tam giác vuông ABC ta có
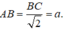
![]()
=> AA' = AB.tan60o = a√3.
Gọi I là tâm của hình chữ nhật BCC’B’ và M là trung điểm của BC. Do tam giác ABC vuông tại A nên M là tâm đường tròn ngoại tiếp tam giác ABC và do đó IM là trục của đường tròn ngoại tiếp đáy ABC và I cách đều B, B’ nên I là tâm của mặt cầu ngoại tiếp lăng trụ. Khi đó ta có:
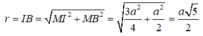

Đáp án C
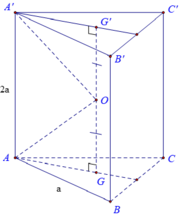
Cho lăng trụ tam giác đều ABC.A'B'C'.
Gọi G, G; lần lượt là tâm của hai đáy ABC và A'B'C'.
Ta có GG' chính là trục của các tam giác ABC và A'B'C' .
Gọi O là trung điểm của GG' thì O cách đều 6 đỉnh của hình lăng trụ
nên là tâm của mặt cầu ngoại tiếp hình lăng trụ. Bán kính mặt cầu là R = OA.
Xét tam giác OAG vuông tại G, ta có:
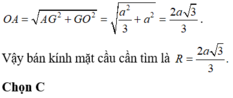
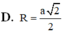


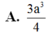
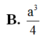
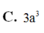
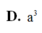
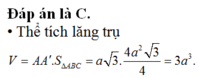
Đáp án B
Gọi O, O’ lần lượt là tâm của các tam giác đều ABC, A’B’C’. Khi đó trung điểm I của OO’ chính là tâm của mặt cầu ngoại tiếp lăng trụ. Bán kính mặt cầu ngoại tiếp lăng trụ là