Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ \(f\left(x\right)+f\left(\frac{1}{x}\right)=x^2\); lần lượt thay \(x=2\) và \(x=\frac{1}{2}\) vào, ta có:
\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\) và \(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\Leftrightarrow3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\)
Giải hệ phương trình với 2 ẩn \(f\left(2\right)\) và \(f\left(\frac{1}{2}\right)\)
Tìm được \(f\left(2\right)=\frac{-13}{32}\)
Ta có \(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\) (1)
Thay \(x\rightarrow\frac{1}{x}\) được \(f\left(\frac{1}{x}\right)+3f\left(x\right)=\frac{1}{x^2}\)
\(\Leftrightarrow3f\left(\frac{1}{x}\right)+9f\left(x\right)=\frac{3}{x^2}\) (2)
Lấy (2) trừ (1) theo vế : \(8f\left(x\right)=\frac{3}{x^2}-x^2\)
\(\Leftrightarrow f\left(x\right)=\frac{1}{8}\left(\frac{3}{x^2}-x^2\right)\)
Vậy f(2) = -13/32

Chọn đáp án C
Phương pháp
Sử dụng công thức nguyên hàm:
![]()
dựa dữ kiện đề bài tìm được C, từ đó tính F(2)-F(-1)
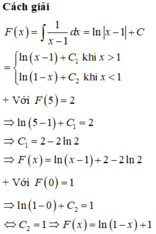


Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.

Ta có:
\(f\left(1\right).f\left(-1\right)=\left(a+b\right).\left(-a+b\right)\)
\(\Rightarrow\left(a+b\right)\left(-a+b\right)=\left(a+b\right)^2\)
\(\Rightarrow-a+b=a+b\)
\(\Rightarrow a=-a\)
\(a\ne0\) thì làm sao có a thỏa mãn được?
Trần Thùy Dung ko biết thì đừng có làm. 5 - 3a - 3b = 5. Bài này trong violympic.

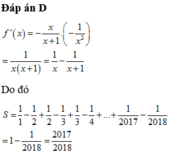

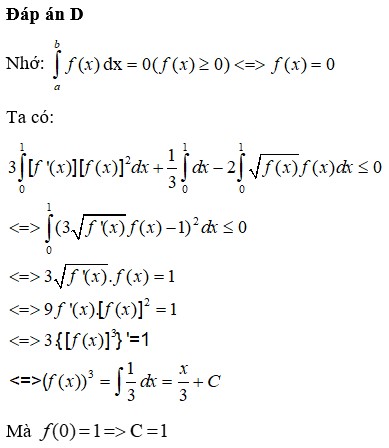
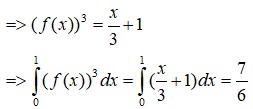
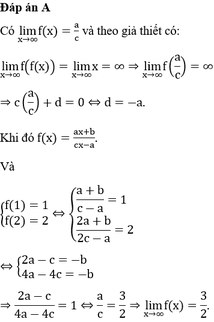

Đáp án D
Ý tưởng bài toán: Với bài toán dạng này, ta thường chọn hai giá trị a, b bất kì, tính tổng f a + f b và tìm mối quan hệ giữa hai giá trị a, b.
f a + f b = log 2 a log 2 a + 1 + log 2 b log 2 b + 1 = 2 log 2 a log 2 b + log 2 a + log 2 b log 2 a + 1 log 2 b + 1
= 2 log 2 a log 2 b + log 2 a + log 2 b log 2 a log 2 b + log 2 a + log 2 b + 1 = 2 log 2 a log 2 b + log 2 a b log 2 a log 2 b + log 2 a b + 1
Cần chọn hai giá trị a, b sao cho tử rút gọn được với mẫu.
Ta thường chọn a+b=k hoặc ab=k. Ở bài toán này ta chọn ab=k.
Nếu a b = 1 4 thì log 2 a b = log 2 1 4 = − 2 .
Suy ra
f a + f b = 2 log 2 a log 2 b − 2 log 2 a log 2 b − 2 + 1 = 2
Vậy với các giá trị a, b thỏa mãn a b = 1 4 thì f a + f b = 2 .
Ta có
S = f 2 − 100 + f 2 − 99 + ... + f 2 − 2 + f 2 0 + f 2 1 + ... + f 2 98
= f 2 − 100 + f 2 98 + f 2 − 99 + f 2 97 + ... + f 2 − 2 + f 2 0 = 2 + 2 + ... + 2 ⏟ 99 s o 2
= 99.2 = 198 .