
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



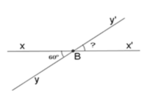
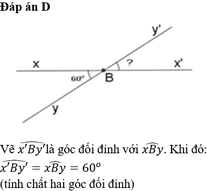
Vì ∠xBy là góc đối đỉnh với ∠x'By'. Khi đó: ∠xBy = ∠x'By' = 60° (tính chất hai góc đối đỉnh)
Chọn đáp án D.

Bạn tự vẽ hình nhé !!!
- TA có : \(\widehat{AMC}=\widehat{BMD}=30\)độ ( Đối đỉnh )
Vì góc AMD và góc BMD kề bù nên :
<=> Góc AMD + góc BMD = 180 độ
<=> góc AMD = 150 độ
b) Cặp đóc đối đỉnh : góc AMC và BMD
góc AMD và BMC
Cặp góc bù nhau : góc ACM và AMD
góc BMD và BMC

1. x O x' y y'
Giải: a) Ta có: \(\widehat{xOy}+\widehat{yOx'}=180^0\) (kề bù)
=> \(\widehat{yOx'}=180^0-\widehat{xOy}=180^0-75^0=105^0\)
Ta lại có: \(\widehat{xOy}=\widehat{x'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOy}=75^0\) => \(\widehat{x'Oy'}=75^0\)
\(\widehat{yOx'}=\widehat{xOy'}\) (đối đỉnh)
Mà \(\widehat{yOx'}=105^0\) => \(\widehat{xOy'}=105^0\)
1b) Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\) (kề bù)
mà \(\widehat{x'Oy}-\widehat{xOy}=30^0\)
=> \(2.\widehat{x'Oy}=210^0\)
=> \(\widehat{x'Oy}=210^0:2=105^0\) => \(\widehat{x'Oy}=\widehat{xOy'}=105^0\) (đối đỉnh)
=> \(\widehat{xOy}=180^0-105^0=75^0\) => \(\widehat{xOy}=\widehat{x'Oy'}=75^0\) (đối đỉnh)
2. O x y x' y' m m'
Giải: a) Ta có: \(\widehat{xOm}=\widehat{x'Om'}\) (đối đỉnh)
\(\widehat{mOy}=\widehat{m'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOm}=\widehat{mOy}\) (gt)
=> \(\widehat{x'Om'}=\widehat{m'Oy'}\)
Ta lại có: \(\widehat{xOy}=\widehat{x'Oy'}\) (đối đỉnh)
Mà \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}.\widehat{xOy}\) (vì Om là tia p/giác)
=> \(\widehat{x'Om'}=\widehat{m'Oy'}=\frac{1}{2}.\widehat{xOy}\)
=> Om' nằm giữa Ox' và Oy'
=> Om' là tia p/giác của góc x'Oy'
b) Tự viết

Bài 1 : giả sử :
Góc 1 = 47
góc 2 = 47 ( đối đỉnh vs góc 1 )
góc 3 = 133 ( kề bù vs góc 1)
góc 4 = 133 ( đối đỉnh vs góc 3)