Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ công thức truy hồi ta có:
\(x_{n+1}>x_n,\forall n=1,2...\)
\(\Rightarrow\)dãy số \(\left(x_n\right)\) là dãy số tăng
giả sử dãy số \(\left(x_n\right)\) là dãy bị chặn trên \(\Rightarrow limx_n=x\)
Với x là nghiệm của pt ta có: \(x=x^2+x\Leftrightarrow x=0< x_1\) (vô lý)
=> dãy số \(\left(x_n\right)\) không bị chặn hay \(limx_n=+\infty\)
Mặt khác: \(\frac{1}{x_{n+1}}=\frac{1}{x_n\left(x_n+1\right)}=\frac{1}{x_n}-\frac{1}{x_n+1}\)
\(\Rightarrow\frac{1}{x_n+1}=\frac{1}{x_n}-\frac{1}{x_n+1}\)
\(\Rightarrow S_n=\frac{1}{x_1}-\frac{1}{x_{n+1}}=2-\frac{1}{x_{n+1}}\)
\(\Rightarrow limS_n=2-lim\frac{1}{x_{n+1}}=2\)

a)
\(u_1=5\)
\(u_2-u_1=1\)
\(u_3-u_2=4\)
............
\(u_n-u_{n-1}=3\left(n-1\right)-2=3n-5\)
Cộng từng vế của đẳng thức và rút gọn ta được:
\(u_n=5+1+4+7+...+3n-5\)
\(=5+\dfrac{\left(3n-5+1\right)\left(n-1\right)}{2}=5+\dfrac{\left(3n-4\right)\left(n-1\right)}{2}\).
Vậy \(u_n=5+\dfrac{\left(3n-4\right)\left(n-1\right)}{2}\) với \(n\ge1\).
Xét hiệu:
\(u_1=5\)
\(u_n-u_{n-1}=3n-5\) \(\left(n\ge2\right)\)
Với \(n\ge2\) thì \(3n-5>0\) nên \(u_n>u_{n-1}\).
Vậy \(\left(u_n\right)\) là dãy số tăng.
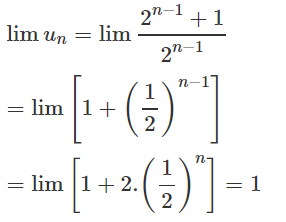
Đáp án B