Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do mạch chỉ có L nên u và i luôn vuông pha nhau.
Phương trình của i có dạng: (1)
và Phương trình của i có dạng: (2)
Từ (1) và (2) suy ra
Ta có hệ :
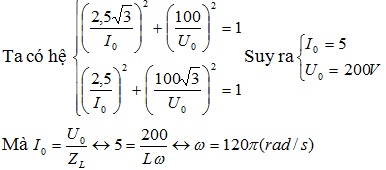

Ta có: \(\left(\frac{v}{x}\right)'=\frac{v^2-ax}{v^2}\)
Mà: \(a=-\omega^2x\) nên \(\left(\frac{v}{x}\right)'=1+\frac{\omega^2x}{v^2}=1+\frac{x^2}{\frac{v^2}{\omega^2}}=1+\frac{x^2}{A^2-x^2}\)
Đạo hàm 2 vế biểu thức đã cho ta có:
\(1+\frac{x_1^2}{A^2-x_1^2}+1+\frac{x_2^2}{A^2-x_2^2}=1+\frac{x_3^2}{A^2-x_3^2}\)
Thay số vào ta tìm đc giá trị \(x_0\)

\(U^2=U_R^2+U_C^2\)
\(\Rightarrow120^2=U_R^2+96^2\)
\(\Rightarrow U_R=72V\)

Mạch chỉ có tụ điện (hoặc cuộn cảm) thì u vuông pha với i
\(\Rightarrow\left(\frac{u}{U_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)

Đáp án là D, vì hai điểm trên dây dao động ngược pha thì cách nhau: (k+0,5)λ

Đáp án đúng rõ ràng là D rồi, vì đây là sự khác biệt nhất khi so sánh dao động cưỡng bức với dao động duy trì.
Nhận xét riêng: Câu hỏi này là rất mơ hồ, cá nhân mình đánh giá thấp ý nghĩa của câu hỏi này.
Bằng miệng