Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của công chúa sinh đôi - Toán lớp 6 | Học trực tuyến
https://h.vn/hoi-dap/question/254152.html
#)Giải :
Ta có : \(\frac{\left(-5\right)^2}{102}=\frac{25}{102}\)
Đặt \(B=\frac{25}{102}\)
Xét \(A=\frac{1919\times161616}{323232\times3838}=\frac{1919\times161616}{1919\times2\times161616\times2}=\frac{1}{2\times2}=\frac{1}{4}\)
Vì \(\frac{1}{4}=\frac{25}{100}>\frac{25}{102}\Rightarrow A>B\)
#~Will~be~Pens~#

|x+3|=|-9|
TH1: x+3=9 => x=9-3 TH2: x+3=-9=> x=-9 -3
x=6 x=-12

Vậy thì sửa lại đề là \(\frac{102}{103}\) và \(\frac{103}{104}\)
Bg
Ta có: \(\text{}\frac{102}{103}+\frac{1}{103}=1\)và \(\frac{103}{104}+\frac{1}{104}=1\)
Vì \(\frac{1}{103}>\frac{1}{104}\)
Nên \(\frac{102}{103}< \frac{103}{104}\)
Vậy \(\frac{102}{103}< \frac{103}{104}\)
102/103 + 1/103 = 1 => 102/103 + 2/206 = 1
103/105 +2/105 = 1
2/105 > 2/206
=> 102/103 < 103/105

Ta có: 100+101/101+102
= 100/101+102 + 101/101+102
Vì 100/101>100/101+102
101/102 > 101/101+102
=>100/101+101/102 > 100+101/101+102

\(a,\frac{3}{-4}\)và \(\frac{-1}{-4}\)
\(\frac{3}{-4}< \frac{-1}{-4}\)
\(b,\frac{15}{17}\)và \(\frac{25}{27}\)
\(\frac{15}{17}< \frac{25}{27}\)

Ta có: 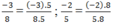
Vì (-3).5 > 8 . (-2) nên 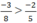
Với hai phân số 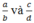 (a, b, c, d ∈ Z ; b > 0 ; d > 0) nếu
(a, b, c, d ∈ Z ; b > 0 ; d > 0) nếu 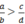 thì ad > bc hoặc
thì ad > bc hoặc 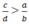 thì cb > ad
thì cb > ad
Ta chứng minh: 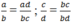
Ta có: 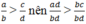
Theo quy tắc so sánh hai phân số ta có: ad > bc
Theo chiều ngược lại, ta cũng có:
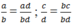
Theo quy tắc so sánh hai phân số nếu 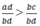
Suy ra 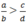

a) -4/27 = -136/918
-37/102 = -333/918
Mà: -136/918 > -333/918
=> -4/27 > -37/102
b) -14/35 = -2/5 = -26/65
Mà -26/65 = -26/65
=> -14/35 = -26/65
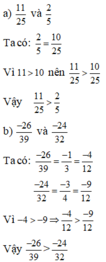
Ta có A = \(\dfrac{1919.161616}{323232.3838}=\dfrac{1919.161616}{2.1919.2.161616}=\dfrac{1}{2.2}=\dfrac{1}{4}\)
Vì\(\dfrac{1}{4}=\dfrac{25}{100}\) , mà \(\dfrac{25}{100}>\dfrac{25}{102}=>A>B\)
Ta có : \(A=\dfrac{1919\cdot161616}{323232\cdot3838}=\dfrac{1\cdot1}{2\cdot2}=\dfrac{1}{4}\)
Giả sử \(A=\dfrac{1}{4}=\dfrac{25}{100}\), mà \(\dfrac{25}{100}>\dfrac{25}{102}\)
\(\Rightarrow\) \(\dfrac{1}{4}>\dfrac{25}{102}\)
\(\Rightarrow\) \(A>B.\)