QT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Vì \(\left\{ \begin{array}{l}JC \bot AE\\BH \bot AE\end{array} \right. \Rightarrow JC//BH\). Vì \(JC//BH \Rightarrow \widehat {HBA} = \widehat {JCA}\) (hai góc đồng vị)
hay \(\widehat {HBA} = \widehat {DCB}\)
Xét \(\Delta ABH\) và \(\Delta DCB\) có:
\(\widehat {HBA} = \widehat {DCB}\) (chứng minh trên)
\(\widehat {AHB} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta ABH\backsim\Delta DCB\) (g.g)
b) Vì (hai góc tương ứng) hay \(\widehat {EAB} = \widehat {CDB}\).
Xét \(\Delta AEB\) và \(\Delta DCB\) có:
\(\widehat {EAB} = \widehat {CDB}\) (chứng minh trên)
\(\widehat {ABE} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta AEB\backsim\Delta DCB\) (g.g)
Suy ra, \(\frac{{BE}}{{BC}} = \frac{{BA}}{{BD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Hay \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\) (điều phải chứng minh).
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
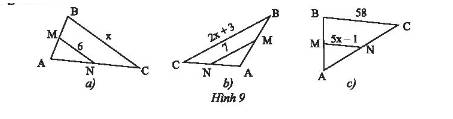
- Hình a:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}x \Leftrightarrow 6 = \frac{1}{2}x \Leftrightarrow x = 6:\frac{1}{2} = 12\)
- Hình b:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow 7 = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow \left( {x + 3} \right) = 7:\frac{1}{2} = 14\)
\( \Rightarrow x = 14 - 3 \Leftrightarrow x = 11\).
- Hình c
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\[\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}.58 \Leftrightarrow \left( {5x - 1} \right) = \frac{1}{2}.58\]
\[ \Leftrightarrow \left( {5x - 1} \right) = 29 \Leftrightarrow 5x = 30 \Leftrightarrow x = 30:5 \Leftrightarrow x = 6\].
13 tháng 9 2023
a: MN là đường trung bình
=>MN=BC/2
=>x=6*2=12
b: MN là đường trung bình
=>2x+3=2*7=14
=>2x=11
=>x=11/2
c: MN là đường trung bình
=>5x-1=58/2=29
=>5x=30
=>x=6
B
1
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
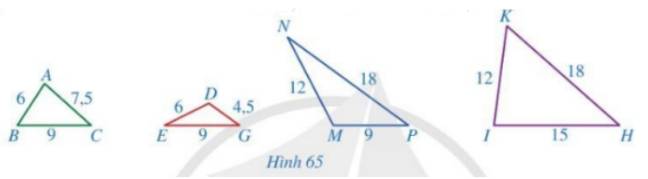
Xét tam giác ABC và tam giác IKH có:
\(\frac{{AB}}{{IK}} = \frac{{AC}}{{IH}} = \frac{{BC}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta ABC \backsim\Delta IKH\) (c-c-c)
Xét tam giác DEG và tam giác MNP có:
\(\frac{{DE}}{{MN}} = \frac{{DG}}{{MP}} = \frac{{EG}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta DEG \backsim\Delta MNP\) (c-c-c)
HQ
Hà Quang Minh
Giáo viên
12 tháng 1 2024
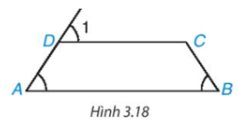
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).
QT
1
11 tháng 9 2023
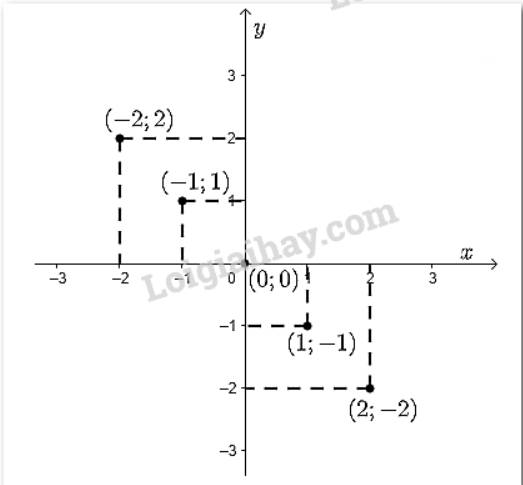
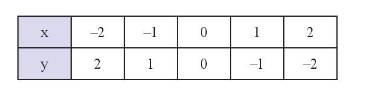
Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2;2} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1; - 1} \right);\left( {2; - 2} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây:
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
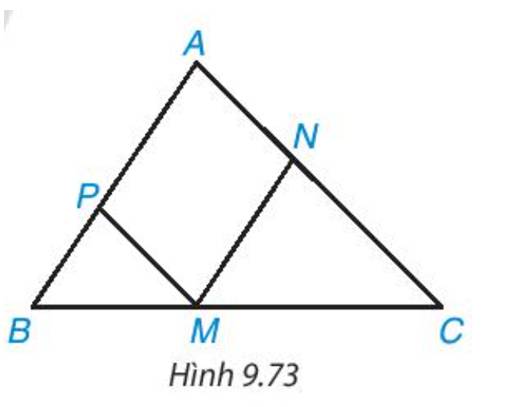
- ΔCNM ~ ΔCAB (vì MN // AB) (1)
- ΔMPB ~ ΔCAB (vì MP // AC) (2)
- Từ (1) và (2) => ΔCNM ~ ΔMPB
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
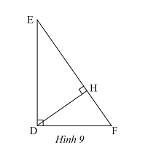
a) Xét \(\Delta DEF\) và \(\Delta HDF\) có:
\(\widehat F\) chung
\(\widehat {EDF} = \widehat {DHF} = 90^\circ \)
Do đó, \(\Delta DEF\backsim\Delta HDF\) (g.g)
b) Vì \(\Delta DEF\backsim\Delta HDF\) nên \(\frac{{DF}}{{HF}} = \frac{{FE}}{{DF}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
\( \Rightarrow D{F^2} = FH.FE\).
c) Theo câu b ta có:
\(D{F^2} = FH.FE\)
Thay số, \(D{F^2} = 5,4.15 = 81 \Rightarrow DF = \sqrt {81} = 9cm\)
Vậy \(DF = 9cm\).
11 tháng 1 2023
a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
Ta có:
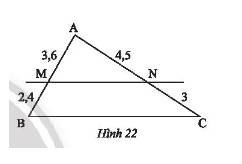
\(\frac{{AM}}{{MB}} = \frac{{3,6}}{{2,4}} = \frac{3}{2}\);\(\frac{{AN}}{{NC}} = \frac{{4,5}}{3} = \frac{3}{2}\).
Vì \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} = \frac{3}{2}\)
Theo định lí Thales đảo trong \(\Delta ABC\), ta có \(MN//BC\) (điều phải chứng minh).