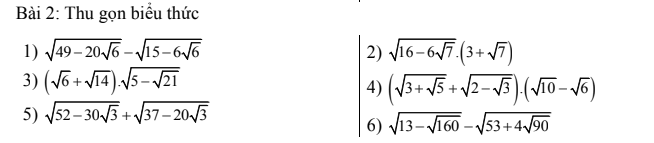K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
1
BH
1 tháng 3 2020
\(3x+3+\sqrt{x^3-x+1}-1=0\)
\(3\left(x+1\right)+\frac{x\left(x+1\right)\left(x-1\right)}{\sqrt{x^3-x+1}}=0\)
\(\left(x+1\right)\left(3+\frac{x\left(x-1\right)}{\sqrt{x^3-x+1}}\right)=0\)
Đk :\(-1\le x\le0,x\ge1\)
Kết hợp điều kiện ta được \(\left(3+\frac{x\left(x-1\right)}{\sqrt{x^3-x+1}}\right)\ge0\)
vậy x = - 1
DH
1
25 tháng 9 2021
1: \(\sqrt{\dfrac{1}{200}}=\dfrac{\sqrt{2}}{20}\)
2: \(\dfrac{5}{1-\sqrt{6}}=-1-\sqrt{6}\)
3: \(\dfrac{1}{1-\sqrt{2}}-\dfrac{1}{1+\sqrt{2}}\)
\(=\dfrac{1+\sqrt{2}-1+\sqrt{2}}{-1}\)
\(=-2\sqrt{2}\)
DH
3
27 tháng 9 2021
2: Ta có: \(\sqrt{16-6\sqrt{7}}\cdot\left(3+\sqrt{7}\right)\)
\(=\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)\)
=9-7
=2
3: Ta có: \(\left(\sqrt{6}+\sqrt{14}\right)\cdot\sqrt{5-2\sqrt{21}}\)
\(=\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)\)
=7-3
=4
27 tháng 9 2021
\(1,=\sqrt{\left(5+2\sqrt{6}\right)^2}-\sqrt{\left(3-\sqrt{6}\right)^2}=5+2\sqrt{6}-3+\sqrt{6}=2+3\sqrt{6}\\ 2,=\sqrt{\left(3-\sqrt{7}\right)^2}\left(3+\sqrt{7}\right)=\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)=9-7=2\\ 3,=\left(\sqrt{3}+\sqrt{7}\right)\sqrt{10-2\sqrt{21}}=\left(\sqrt{3}+\sqrt{7}\right)\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}\\ =\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)=7-3=4\\ 4,=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{6+2\sqrt{5}}+\sqrt{4-2\sqrt{3}}\right)\\ =\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+1+\sqrt{3}-1\right)\\ =\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=5-3=2\)
\(5,\\ =\sqrt{\left(3\sqrt{3}-5\right)^2}+\sqrt{\left(5-2\sqrt{3}\right)^2}=3\sqrt{3}-5+5-2\sqrt{3}=\sqrt{3}\\ 6,=\sqrt{13-4\sqrt{10}}-\sqrt{53+12\sqrt{10}}\\ =\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}-\sqrt{\left(3\sqrt{5}-2\sqrt{2}\right)^2}\\ =2\sqrt{2}-\sqrt{5}-3\sqrt{5}+2\sqrt{2}=4\sqrt{2}-4\sqrt{5}\)
TN
8 tháng 3 2018
Gọi số thứ nhất là x
\(\Rightarrow\)Số thứ hai là 19-x
Theo đề bài ta có phương trình:
x2+(19-x)2=185
\(\Leftrightarrow x^2+361-38x+x^2=185\)
\(\Leftrightarrow2x^2-38x+361-185=0\)
\(\Leftrightarrow2x^2-38x+176=0\)
\(\Leftrightarrow x^2-19x+88=0\)
\(\Leftrightarrow x^2-11x-8x+88=0\)
\(\Leftrightarrow x\left(x-11\right)-8\left(x-11\right)=0\)
\(\Leftrightarrow\left(x-11\right)\left(x-8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-11=0\\x-8=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=11\\x=8\end{cases}}\)
Vậy số thứ nhất là 8, số thứ hai là 19-8=11 hoặc số thứ nhất là 11, số thứ hai là 19-11=8
7 tháng 10 2015
\(=\sqrt{3\left(x^2-2x+1\right)+25}\supseteq\sqrt{3\left(x+1\right)^2+25}\supseteq5\)
min=5 <=>x=-1
MT
7 tháng 10 2015
\(\text{Đặt }A=\sqrt{3x^2-6x+28}=\sqrt{3x^2-6x+3+25}\)
\(=\sqrt{3.\left(x^2-2x+1\right)+25}=\sqrt{3.\left(x-1\right)^2+25}\)
\(\Rightarrow A^2=3.\left(x-1\right)^2+25\ge25\Rightarrow A\ge\sqrt{25}=5\)
Dấu "=" xảy ra khi : x=1
Vậy GTNN của A là 5 tại x=1
23 tháng 9 2021
Áp dụng tslg của góc nhọn trong tam giác ABH vuông tại H:
\(sinB=\dfrac{AH}{AB},cosB=\dfrac{BH}{AB},tanB=\dfrac{AH}{BH},cotB=\dfrac{BH}{AH}\)
Áp dụng tslg của góc nhọn trong tam giác AHC vuông tại H :
\(sinC=\dfrac{AH}{AC},cosC=\dfrac{HC}{AC},tanC=\dfrac{AH}{HC},cotC=\dfrac{HC}{AH}\)
23 tháng 9 2021
\(\sin B=\dfrac{AH}{AB};\cos B=\dfrac{BH}{AB};\tan B=\dfrac{AH}{BH};\cot B=\dfrac{BH}{AH}\\ \sin C=\dfrac{AH}{AC};\cos C=\dfrac{CH}{AC};\tan C=\dfrac{AH}{HC};\cot C=\dfrac{HC}{AH}\)
23 tháng 9 2021
\(\tan B=\dfrac{AC}{AB}=\dfrac{5}{12}\Rightarrow AC=\dfrac{5\cdot6}{12}=2,5\left(cm\right)\\ BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+2,5^2}=6,5\left(cm\right)\)
23 tháng 9 2021
Áp dụng tslg của góc nhọn trong tam giác ABC vuông tại A:
\(tanB=\dfrac{AC}{AB}=\dfrac{5}{12}\)
\(\Rightarrow\dfrac{AC}{6}=\dfrac{5}{12}\Rightarrow AC=2,5\left(cm\right)\)
Xét tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Rightarrow BC^2=6^2+\left(2,5\right)^2=42,25\Rightarrow BC=6,5\left(cm\right)\)