
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mình tìm không tháy bạn ơi ~ chủ yếu là mình nhờ mấy bạn từng học qua rồi chỉ giúp những dạng chủ yếu,mẹo vặt các loại đấy bạn !! không phải mình tìm đề đâu ~~`

Bài 2:
a: Ta có: \(M=2x\left(2x^3-3x\right)-x^2\left(3x^2-2\right)-x^2\left(x^2-4\right)\)
\(=4x^4-6x^2-3x^4+2x^2-x^4+4x^2\)
=0
b: Ta có: \(N=x\left(y^2-x\right)-y\left(xy-x^2\right)-x\left(xy-x-1\right)\)
\(=xy^2-x^2-xy^2+x^2y-x^2y+x^2+x\)
\(=x\)

\(10,\\ a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\\ \Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2\ge4ab+4ac+4ad+4ae\\ \Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae+4e^2\right)\ge0\\ \Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow\dfrac{a}{2}=b=c=d=e\)
\(4,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{4}\left(2a^2+2b^2+2c^2-2ab-2ac-2bc\right)\ge3ab+3bc+3ca\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{2}a^2-\dfrac{1}{2}b^2-\dfrac{1}{2}c^2-ab-bc-ac\ge0\\ \Leftrightarrow\dfrac{1}{2}a^2+\dfrac{1}{2}b^2+\dfrac{1}{2}c^2+ab+ac+bc\ge0\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge0\\ \Leftrightarrow\left(a+b+c\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a+b+c=0\)



a) \(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{10}=\dfrac{y}{15}\\\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{15}=\dfrac{z}{21}\end{matrix}\right.\Rightarrow\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{10}=2\Rightarrow x=2.10=20\\\dfrac{y}{15}=2\Rightarrow y=2.15=30\\\dfrac{z}{21}=2\Rightarrow z=2.21=42\end{matrix}\right.\)

\(x^2-3x+1\)
\(=x^2-2.x.\frac{3}{2}+\frac{9}{4}-\frac{5}{4}\)
\(=\left(x-\frac{3}{2}\right)^2-\frac{5}{4}\)
\(=\left(x-\frac{3}{2}-\frac{\sqrt{5}}{2}\right)\left(x-\frac{3}{2}+\frac{\sqrt{5}}{2}\right)\)

\(Q=x^2+y^2-4x-y+7\)
\(=x^2-4x+4+y^2-y+\dfrac{1}{4}+\dfrac{11}{4}\)
\(=\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\forall x,y\)
Dấu '=' xảy ra khi x=2 và \(y=\dfrac{1}{2}\)

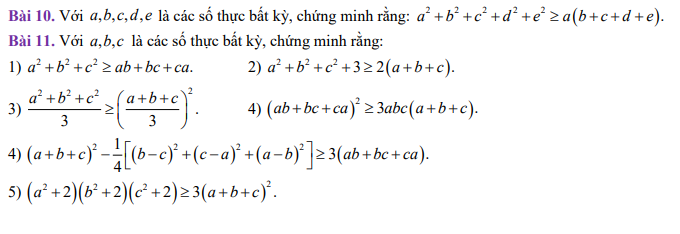




Cau 2