Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

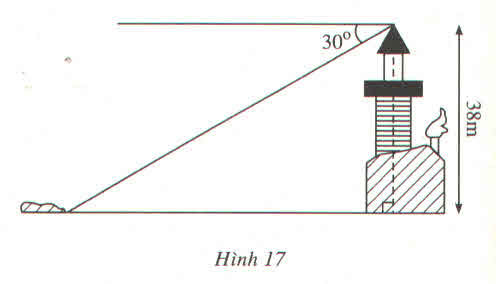
*gọi: A là đỉnh ngọn đèn biển; B là chân đèn; C là hòn đảo
>>tam giác ABC vuông tại B có: AB=38m; góc ACB=30 độ
>>khoảng cách từ đảo đến chân đèn:
AC=AB/tan30=38/tan30=38căn3=65,8179m

Khoảng cách từ đảo đến chân đèn là:
\(38\cdot\cot30^0\simeq65,818\left(cm\right)\)

Khoảng cách từ đảo đến chân cột đèn biển là cạnh kề với góc 30 ° , chiều cao của cột đèn biển là cạnh đối diện với góc 30 °
Vậy khoảng cách từ đảo đến chân đèn là:
38.cotg 30 ° ≈ 65,818 (cm)

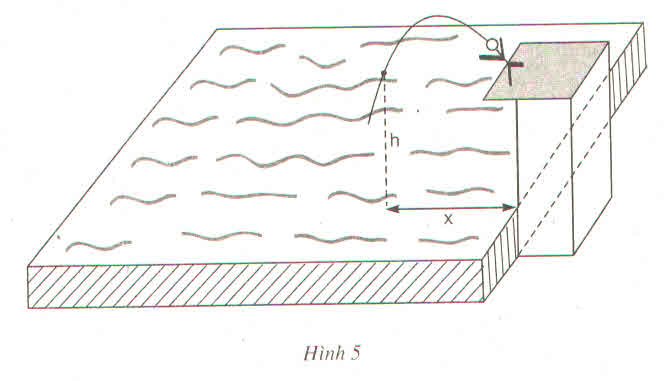
a) \(3=-\left(x-1\right)^2+4\Leftrightarrow x^2-2x=0\)
Suy ra \(x_1=0;x_2=2\)
b) Khi vận động viên chạm mặt nước thì \(h=0\).
Do đó \(-\left(x-1\right)^2+4=0\) hay \(x^2-2x-3=0\)
Suy ra \(x_1=-1;x_2=3\)
Vì khoảng cách không âm nên \(x_2=3\left(m\right)\)

Cho ΔABC cân tại A có AB=AC=3cm; BC=4cm
BH=1/2BC=1/2x4=2(cm)
Xét ΔABH vuông tại H có \(\cos B=\dfrac{BH}{AB}=\dfrac{2}{3}\)
nên \(\widehat{B}\simeq48^011'\)
=>Góc cần tìm có số đo là \(1^049'\)

a) \(I=\frac{U}{R_{td}}=\frac{U}{R_1+R_2}=\frac{12}{45+15}=0,2\left(A\right)\)
\(P=UI=12.0,2=2,4\) ( W )
b) Đèn sáng bth. Vì \(U_1=U-U_2=U-I_2.R_2=U-I.R_2=12-0,2.15=9=U_{den}\)
\(A=P.t=2,4.600=1440\left(J\right)\)