Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2:
\(x=-3\cdot cos\left(2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(pi+2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(2pi\cdot t+2pi\right)\)
Biên độ là A=3
Tần số góc là 2pi
Chu kì là T=2pi/2pi=1
Pha ban đầu là 2pi
Pha của dao động tại thời điểm t=0,5 giây là;
\(2pi\cdot0.5+2pi=3pi\)
bài 1:
Biên độ góc: A = 5 cm
Tần số góc = 10 pi
Chu kì T = 2pi / tần số góc = 0,2 s
pha dao động là 10 pi x 1 - pi /2 = 19/ 2 pi

Biên độ: A=3
Tần số góc: pi
Chu kì: T=2pi/pi=2
Pha dao động: pi*t
Pha ban đầu: 2pi

Biên độ: A=8
Pha ban đầu: pi
Chu kì: \(T=\dfrac{2pi}{4pi}=\dfrac{1}{2}\)
Tần số góc là 4pi

Pha ban đầu là \(4pi\cdot t-\dfrac{pi}{2}\)
Tần số là \(f=\dfrac{4pi}{2pi}=2\)
Chu kì là \(T=\dfrac{1}{f}=\dfrac{1}{2}\)
Tần số góc là \(w=2pi:\dfrac{1}{2}=4pi\)

Biên độ: A=0,1
tần số góc: 180pi
Chu kì: T=2pi/180pi=1/90
Pha ban đầu: 2pi

Chu kì dao động là: \(T=\dfrac{1}{f}=\dfrac{1}{5}=0,2\left(s\right)\)
Tần số góc của dao động là: \(\omega=2\pi f=10\pi\left(rad/s\right)\)
Lúc t = 0, ta có: \(\left\{{}\begin{matrix}x=A\\v=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}cos\varphi=1\\sin\varphi=0\end{matrix}\right.\Rightarrow\varphi=0\)
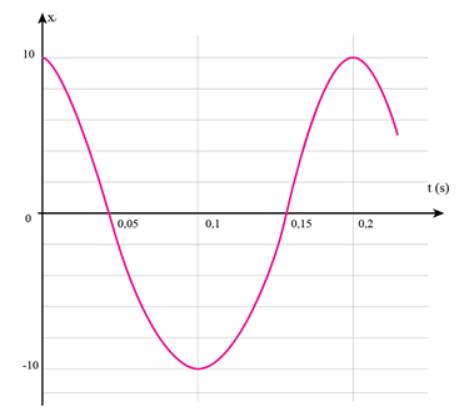
Phương trình dao động là: \(x=10cos\left(10\pi t\right)cm\)
Vẽ đồ thị:
`a)` Biên độ dao động `A=2`
Pha ban đầu dao động `\varphi =\pi/2`
`b)` Pha dao động khi `t=2` là `4\pi .2+\pi/2 = [17\pi]/2`
Li độ dao động khi `t=2` là `x=2cos ([17\pi]/2)=0`