HT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Y
6 tháng 6 2023
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\)
\(=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}^2+2\sqrt{x}+1^2}-\dfrac{\sqrt{x}+2}{\sqrt{x}^2-1^2}\right).\dfrac{x-1}{2\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{x-1}{2\sqrt{x}}\)
Tới đây là có được mẫu chung ở dấu = thứ 2 rồi.
LD
6 tháng 6 2023
\(A=\left(\dfrac{\sqrt{x}-2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}+2}{x-1}\right):\dfrac{2\sqrt{x}}{x-1}\) ( với x>0;\(x\ne1\) )
\(=\left[\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right].\dfrac{x-1}{2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(x-1\right)}.\dfrac{x-1}{2\sqrt{x}}\)
\(=.....\) ( theo như trên )
7 tháng 6 2018
1/ Đặt \(\hept{\begin{cases}\sqrt{x-2013}=a\\\sqrt{x-2014}=b\end{cases}}\)
Thì ta có:
\(\frac{\sqrt{x-2013}}{x+2}+\frac{\sqrt{x-2014}}{x}=\frac{a}{a^2+2015}+\frac{b}{b^2+2014}\)
\(\le\frac{a}{2a\sqrt{2015}}+\frac{b}{2b\sqrt{2014}}=\frac{1}{2\sqrt{2015}}+\frac{1}{2\sqrt{2014}}\)
7 tháng 6 2018
2/ \(\frac{x}{2x+y+z}+\frac{y}{x+2y+z}+\frac{z}{x+y+2z}\)
\(\le\frac{1}{4}\left(\frac{x}{x+y}+\frac{x}{x+z}+\frac{y}{y+x}+\frac{y}{y+z}+\frac{z}{z+x}+\frac{z}{z+y}\right)\)
\(=\frac{3}{4}\)
26 tháng 12 2019
nhầm
phân thức cuối là:\(\frac{c^2-ab}{2c^2+a^2+b^2}\)
giúp mình nha
T
26 tháng 12 2019
Làm như thầy bạn bảo nhé!
BĐT \(\Leftrightarrow\Sigma_{cyc}\frac{2a^2-2bc}{2a^2+b^2+c^2}\ge0\) (nhân 2 vào 2 vế) (*)
\(VT_{\text{(*)}}=\Sigma_{cyc}\left(1-\frac{b^2+c^2+2bc}{2a^2+b^2+c^2}\right)=3-\Sigma_{cyc}\frac{\left(b+c\right)^2}{2a^2+b^2+c^2}\)
\(\ge3-\Sigma_{cyc}\left(\frac{b^2}{a^2+b^2}+\frac{c^2}{a^2+c^2}\right)=0\)
6 tháng 1 2019
\(x+y=2\Rightarrow y=2-x\)
\(xy=x.\left(2-x\right)=2x-x^2=-\left(x^2-2x\right)\)
\(=-\left(x^2-2x+1-1\right)=-\left(x-1\right)^2+1=1-\left(x-1\right)^2\le1\)
=> đpcm
( Dấu "=" xảy ra <=> x = 1 => y = 2 - x = 2 - 1 = 1 )
30 tháng 10 2019
A B C E F I H
gọi H là trực tâm các đường cao BI,CF,AE
Ta có : \(\cot A=\frac{AI}{BI}=\frac{AF}{FC}\) ; \(\cot B=\frac{BE}{AE}=\frac{BF}{FC}\); \(\cot C=\frac{CI}{BI}=\frac{CE}{AE}\)
\(\Rightarrow\cot A.\cot B+\cot B.\cot C+\cot C.\cot A=\frac{AI}{BI}.\frac{BE}{AE}+\frac{BF}{FC}.\frac{CI}{BI}+\frac{CE}{AE}.\frac{AF}{FC}\)
\(\Delta AFH~\Delta AEB\left(g.g\right)\Rightarrow\frac{AF}{AH}=\frac{AE}{AB}\Rightarrow\frac{AF}{AE}=\frac{AH}{AB}\)
\(\Rightarrow\frac{CE}{AE}.\frac{AF}{FC}=\frac{CE.AH}{AB.CF}=\frac{S_{ACH}}{S_{ABC}}\)
Tương tự : \(\frac{AI}{BI}.\frac{BE}{AE}=\frac{S_{BHA}}{S_{ABC}};\frac{BF}{FC}.\frac{CI}{BI}=\frac{S_{BCH}}{S_{ABC}}\)
\(\Rightarrow\cot A.\cot B+\cot B.\cot C+\cot C.\cot A=\frac{S_{BHA}+S_{BHC}+S_{AHC}}{S_{ABC}}=1\)
2 tháng 1 2020
Giúp mk vs mn ơi. Mk cx chưa cần vội lm trước 22h nha. Yêu mn nhiều lm
29 tháng 6 2021
\(abc\le\left(\frac{a+b+c}{3}\right)^3\Leftrightarrow\sqrt[3]{abc}\le\frac{a+b+c}{3}\)
BĐT Cô- si
30 tháng 5 2021
Ta có \(3a+1\ge\left(\dfrac{\sqrt{10}-1}{3}a+1\right)^2\Leftrightarrow a\left(3-a\right)\ge0\) (luôn đúng)
Do đó \(\sqrt{3a+1}\ge\dfrac{\sqrt{10}-1}{3}a+1\).
Tương tự, \(\sqrt{3b+1}\ge\dfrac{\sqrt{10}-1}{3}b+1;\sqrt{3c+1}\ge\dfrac{\sqrt{10}-1}{3}c+1\).
Do đó \(\sqrt{3a+1}+\sqrt{3b+1}+\sqrt{3c+1}\ge\sqrt{10}+2\).
Dấu "=" xảy ra khi chẳng hạn a = 3; b = c = 0
30 tháng 5 2021
Tham khảo:
https://hoc24.vn/hoi-dap/tim-kiem?id=219071991005&q=Cho%203%20s%E1%BB%91%20th%E1%BB%B1c%20kh%C3%B4ng%20%C3%A2m%20a%2Cb%2Cc%20v%C3%A0%20a%20b%20c%3D3%20T%C3%ACm%20GTLN%20v%C3%A0%20GTNN%20c%E1%BB%A7a%20bi%E1%BB%83u%20th%E1%BB%A9c%20K%3D%5C%28%5Csqrt%7B3a%201%7D%20%5Csqrt%7B3b%201%7D%20%5Csqrt%7B3c%201%7D%5C%29
4 tháng 7 2017
Áp dụng BĐT Cauchy-Schwarz ta có:
\(\dfrac{a}{\sqrt{a^2+1}}=\dfrac{a}{\sqrt{a^2+ab+bc+ca}}=\dfrac{a}{\sqrt{\left(a+b\right)\left(a+c\right)}}\)
\(\le\dfrac{1}{2}\left(\dfrac{a}{a+b}+\dfrac{a}{a+c}\right)\). Thiếp lập 2 BĐT còn lại:
\(\dfrac{b}{\sqrt{b^2+1}}\le\dfrac{1}{2}\left(\dfrac{b}{b+c}+\dfrac{b}{a+b}\right);\dfrac{c}{\sqrt{c^2+1}}\le\dfrac{1}{2}\left(\dfrac{c}{c+a}+\dfrac{c}{b+c}\right)\)
Cộng theo vế 3 BĐT trên ta có:
\(A\le\dfrac{1}{2}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{c+a}{c+a}\right)=\dfrac{1}{2}\cdot3=\dfrac{3}{2}\)
Xảy ra khi \(a=b=c=\dfrac{1}{\sqrt{3}}\)
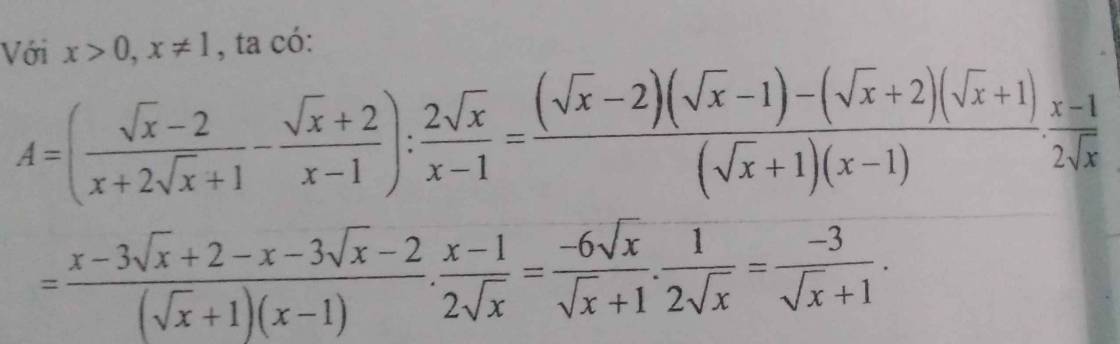
Chứng minh \(\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\ge\dfrac{\left(a+b+c\right)^2}{x+y+z}với\left(x;y;z>0\right)\)
Thường thì sẽ sử dụng cái này nhiều nhất
Đầu tiên đi chứng minh
\(\dfrac{a^2}{x}+\dfrac{b^2}{y}\ge\dfrac{\left(a+b\right)^2}{x+y}\\ \Leftrightarrow\dfrac{a^2y+b^2x}{xy}\ge\dfrac{a^2+2ab+b^2}{x+y}\\ \Leftrightarrow a^2xy+\left(bx\right)^2+\left(ay\right)^2+b^2xy\ge a^2xy+2abxy+b^2xy\\ \Leftrightarrow\left(ay\right)^2+\left(bx\right)^2-2abxy\ge0\Leftrightarrow\left(ay-bx\right)^2\ge0\left(đúng\right)\)
Áp dụng 1 lần nữa ta có điều ở trên
Dấu $=$ xảy ra $⇔\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}$