Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi vẽ hình thứ 3,ta có:
Số hình lập phương đơn vị bên trái là 3.4.3=36
Số hình lập phương đơn vị bên trái là 3.4.3 =36
Số hình lập phương đơn vị ở giữa là 3.3=9
Vậy có tổng số :36+36+9=81 hình lập phương đơn vị
Với quy luật đó thì hình thứ 10:
Số hình lập phương đơn vị bên trái là 10.11.10=1100
Số hình lập phương đơn vị bên trái là 10.11.10=1100
Số hình lập phương đơn vị ở giữa là 10.10 =100
Vậy tổng số hình lập phương đơn vị của hình thứ 10 là:
1100 + 1100 +100=2300 (hình)

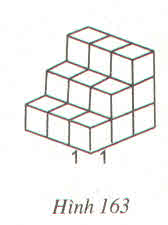
Lớp dưới cùng gồm: 3.3 (hình lập phương đơn vị)
Lớp ở giữa gồm: 3.2 (hình lập phương đơn vị)
Lớp trên cùng: 3 (hình lập phương đơn vị)
Tổng cộng có 9+6+3=18 (hình lập phương đơn vị)

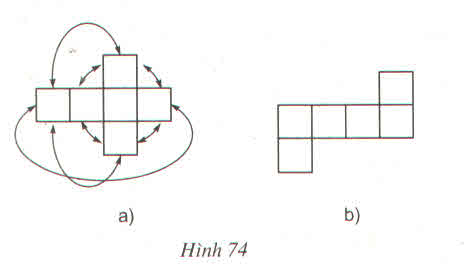
Mỗi hình vuông tương ứng với một mặt của hình lập phương có 6 mặt. Đầu tiên chúng ta giữ cố định một hình vuông ở giữa để làm một mặt trong cùng của hình lập phương, sau đó di chuyển các hình vuông còn lại theo chiều mũi tên như sau để được hình lập phương:

Hình 138 là một hình chóp tam giác đều
Hình 139 là một hình chóp tứ giác đều
Hình 140 là một hình chọp ngũ giác đều
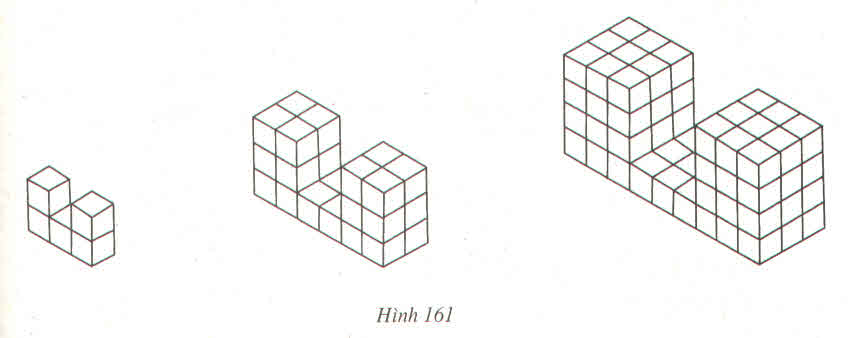







Số hình lập phương ở hình 1: 1.3+1.1.2=5 (khối)
Số hình lập phương ở hình 2:22.3+22.2.2=28 (khối)
Số hình lập phương ở hình 3:32.3+32.3.2=81 (khối)
\(\Rightarrow\)Công tức tính:
Số hình lập phương ở hình x: x2.3+x2.x.2 (khối)
Số hình lập phương ở hình 10 là:102.3+102.10.2=2300 (khối)
Cách 1 : Khi ta vẽ hình thứ tư thì :
Số hình lập phương đơn vị ở phía trái là 4.5.4=80