Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+)Gọi thời gian vật rơi hết quãng đường là t (s)
+) Quãng đường 2 giấy cuối tức là khoảng cách của điểm t-2 s so với mặt đất
+) Ta có
\(\dfrac{t^2}{2}.9,8-\dfrac{\left(t-2\right)^2}{2}.9,8\) = 98
=> t=4 (s)
==> h=\(\dfrac{t2}{2}.9,8\)=78,4 (m)

a)Thời gian vật rơi: \(S=\dfrac{1}{2}gt^2\)
\(\Rightarrow t=\sqrt{\dfrac{2S}{g}}=\sqrt{\dfrac{2\cdot45}{10}}=3s\)
b)Vận tốc vật trước khi chạm đất: \(v=gt=10\cdot3=30m/s\)
c)Quãng đường vật rơi được trong 2s đầu:
\(S=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot2^2=20m\)
Quãng đường vật rơi trong giây cuối cùng:
\(\Delta S=S_3-S_2=45-20=25m\)

Đáp án A
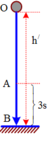
Chọn trục Ox có phương thẳng đứng hướng xuống, gốc tọa độ tại O và gốc thời gian lúc vật bắt đầu rơi. Gọi h là độ cao của vật so với mặt đất và t là thời gian vật rơi, ta có:
![]()
Trước khi chạm đất 2 s, vật đi được quãng đường là h':
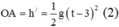
Theo đề, ta có:
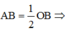
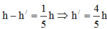
Từ (l) và (2), suy ra:
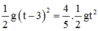
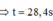
Độ cao ban đầu của vật:
(1) 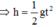
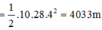

Quãng đường vật đi trong giây cuối cùng là 63,7m.
\(\Rightarrow\) Thời gian rơi của vật trên cae quãng đường:
\(S=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2\)
\(\Rightarrow\dfrac{1}{2}\cdot9,8\cdot t^2-\dfrac{1}{2}\cdot9,8\cdot\left(t-1\right)^2=63,7\Rightarrow t=7\left(s\right)\)
Độ cao S để thả vật rơi: \(S=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot9,8\cdot7^2=240,1\left(m\right)\)
Vận tốc vật lúc chạm đất: \(v=g\cdot t=9,8\cdot7=68,6\)(m/s)

Hướng dẫn giải:
a) \(S=\frac{1}{2}gt^2\)
\(\rightarrow t=\sqrt{\frac{2S}{g}}=2s\)
b) \(v=gt=20\) m/s
Quãng đường vật rơi trong 5s đầu tiên là
S3=1/2.10.52 =125
Quãng đường vật rơi đc trong thời gian t là
S1=1/2.10.t (1)
Quảng đường vật rơi đc trong 2s cuối là
S2=1/2.10.(t-2)2
=> s1-s2=s3
-> t =7.25s thay t vào pt (2) ta đc
S=137.8125m
Còn vận tốc thì áp dụng ct tính ra thôi :))))))

Gọi \(t(s)\) là thời gian vật rơi trên cả quãng đường.
Chọn chiều dương từ trên hướng xuống.
Quãng đường vật rơi trong 0,75s cuối cùng là:
\(\Delta h_1=h-h_1=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-0,75\right)^2=\dfrac{1}{2}g\left(1,5t-0,5625\right)\)
Quãng đường vật rơi trong 0,75s liền trước đó là:
\(\Delta h_2=h_1-h_2=\dfrac{1}{2}g\left(t-0,75\right)^2-\dfrac{1}{2}g\left(t-\left(0,75+0,75\right)\right)^2=\dfrac{1}{2}g\left(1,5t-1,6875\right)\)
Theo bài: \(\Delta h_1=2\Delta h_2\)
\(\Rightarrow\dfrac{1}{2}g\left(1,5t-0,5625\right)=2\cdot\dfrac{1}{2}g\cdot\left(1,5t-1,6875\right)\)
\(\Rightarrow t=0,125s\)
Độ cao ban đầu vật rơi: \(h=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot0,125^2=0,078125\approx0,08m=8cm\)
ta có thể sử dụng hai công thức vật lý cơ bản sau: Độ dài quãng đường (d) với thời gian (t), gia tốc (a) ban đầu và vận tốc (v) ban đầu: d = vt + 0.5a*t^2 Vận tốc (v) với thời gian (t) và gia tốc (a) ban đầu: v = a*t Giả sử vật rơi ban đầu ở độ cao h so với mặt đất. Ta cần tìm h. Trong 0,75s liền trước đó, vật rơi đã đi được một quãng đường d1: d1 = v1t1 + 0.5gt1^2 v1 = gt1 v1 = 10/s^2 * 0,75s = 7,5m/s d1 = 7,5m/s * 0,75s + 0.5*10/s^2 * (0,75s)^2 = 5,625m Trong 0,75s cuối trước khi chạm đất, vật rơi đi được quãng đường gấp đôi d1: d2 = 2*d1 = 11,25m Ta có thể sử dụng lại công thức đầu tiên để tính độ cao h ban đầu: h = d2 + d1 = 11,25m + 5,625m = 16,875m Vậy độ cao ban đầu của vật rơi là 16,875m.
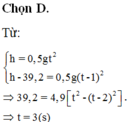
chọn gốc tọa độ, gốc thời gian lúc vật rơi tự do, chiều dương từ trên xuống dưới
quãng đường vật rơi với t giây là
s1=g.t2.0,5=5t2
quãng đường vật rơi với t-2 giây đầu là
s2=g.0,5.(t-2)2=5t2-20t+20
quãng đường vật rơi hai giây cuối là 98m
\(\Rightarrow\Delta s=s_1-s_2=98\)\(\Rightarrow\)t=5,9s
chiều cai ban đầu của vật
s=h=g.t2.0,5=174,05m
bạn có thể giải chi tiết vì sao t = 5,9 s được không