Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 7 :
( bạn đạt A = (...) cái biểu thức đấy nhé, tự đặt )
Ta có :
\(\frac{1}{\sqrt{1}}=\frac{1}{1}>\frac{1}{10}=\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{2}}>\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{3}}>\frac{1}{\sqrt{100}}\)
\(............\)
\(\frac{1}{\sqrt{100}}=\frac{1}{\sqrt{100}}\)
\(\Rightarrow\)\(A=\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{100}}>\frac{1}{\sqrt{100}}+\frac{1}{\sqrt{100}}+\frac{1}{\sqrt{100}}+...+\frac{1}{\sqrt{100}}\)
\(A>\frac{100}{\sqrt{100}}=\frac{100}{10}=10\)
\(\Rightarrow\)\(A>10\)
Vậy \(A>10\)
Chúc bạn học tốt ~
Bạn làm được mình bài 7 thôi à, mình thấy bạn giỏi lắm mà. Mình có tới mấy chục bài cần giải cơ. Dạo này mình hỏi nhiều vì sắp đi thi.

Gợi ý làm bài :
HS tự vẽ hình, viết GT, KL.
a, \(\triangle ABC\) đều vì có AB = AC và \(\widehat{B}=60^{\text{o}}\).
b, Trong một tam giác đều, 3 đường cao bằng nhau (HS tự chứng minh).
Chiều cao của tam giác đều được tính bằng công thức \(h=a\frac{\sqrt{3}}{2}\).
c, HS tự chứng minh.
Nhận xét : Trọng tâm, trực tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp là 4 điểm trùng nhau.

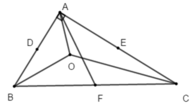
+ Vì O là giao điểm của ba đường phân giác trong tam giác ABC nên O là tâm của đường tròn nội tiếp tam giác ABC nên đáp án A sai.
+ Tam giác ABC vuông tại A có F là trung điểm của BC nên AF là đường trung tuyến ứng với cạnh huyền
Do đó: AF = 1 2 BC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra AF = FC = FB
Nên F cách đều ba đỉnh A, B, C
Do đó F là tâm đường tròn ngoại tiếp tam giác ABC.
+ Vì D ≠ E ≠ F và chỉ có một đường tròn ngoại tiếp tam giác ABC nên đáp án B, C sai và D đúng.
Chọn đáp án D
Gọi M là trung điểm cạnh BC của tam giác ABC vuông tại A ta có MA=MB=MC nêm M là tâm đường tròn ngoại tiếp ABC, với BC là đường kính
M là trung điểm cạnh BC của tam giác ABC vuông tại A ta có MA=MB=MC nên M là tâm đường tròn ngoại tiếp ABC với BC là đường kính